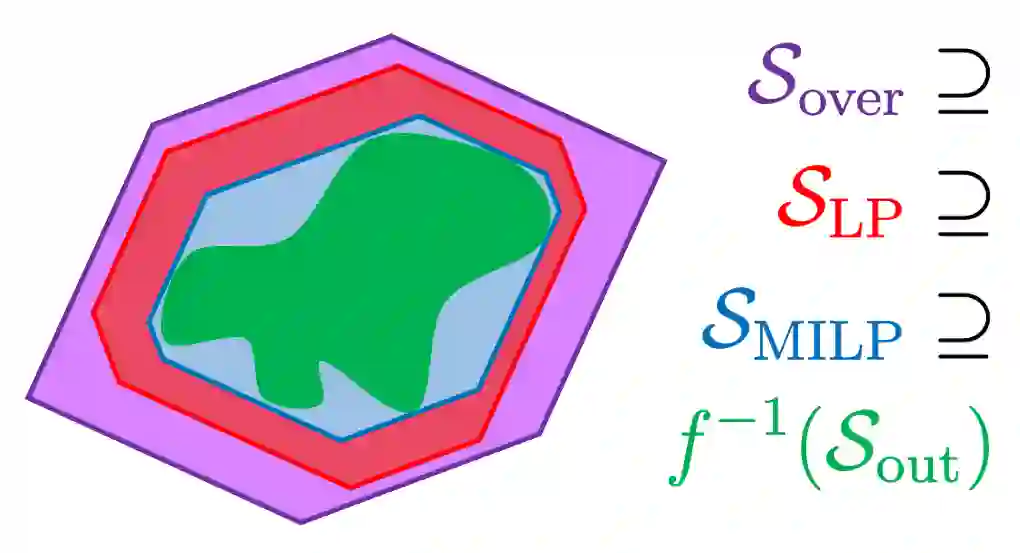
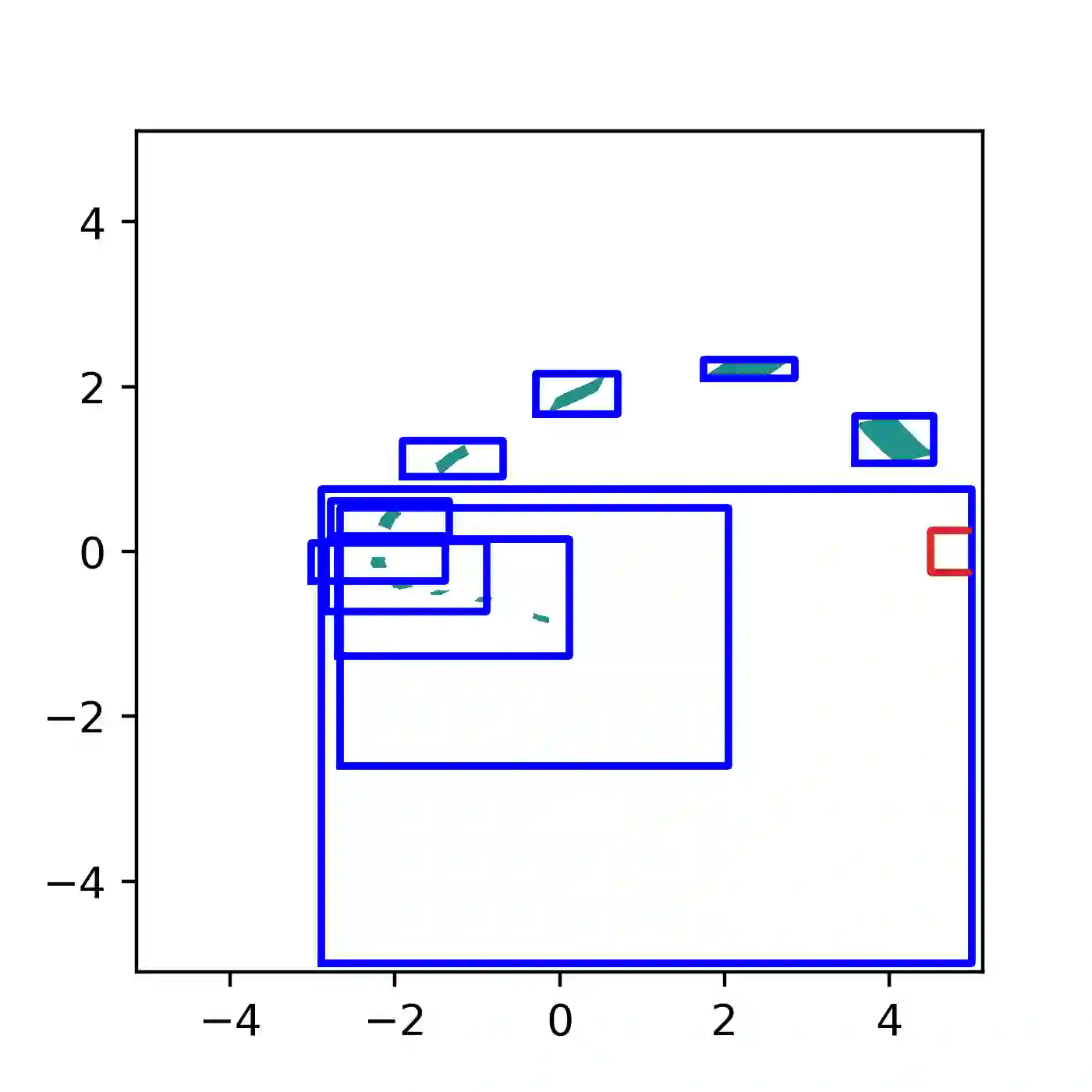
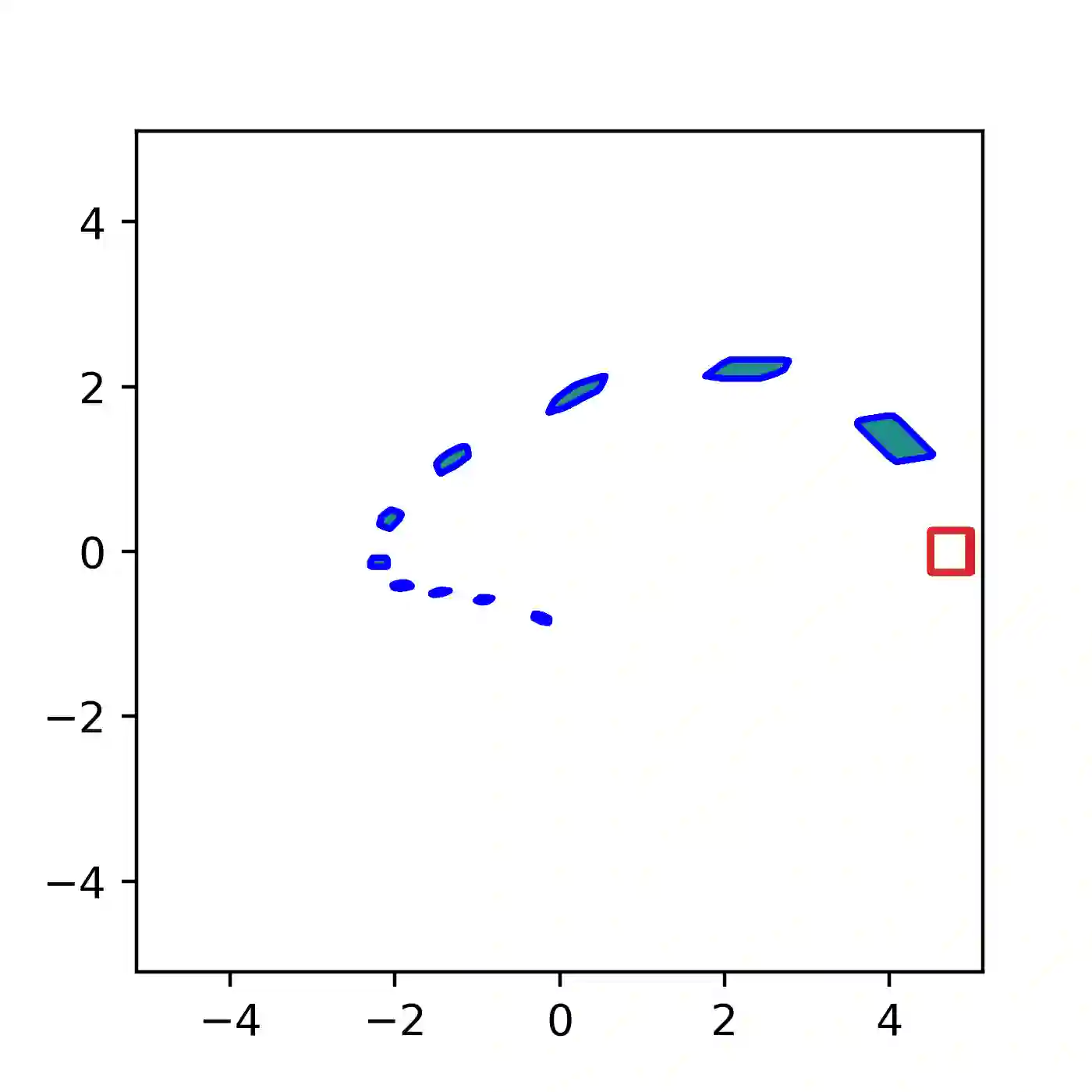
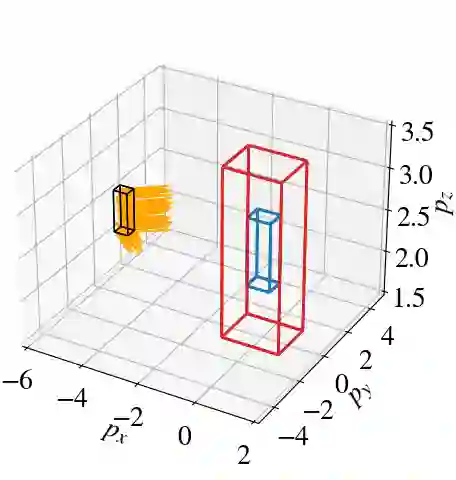
Most work on the formal verification of neural networks has focused on bounding the set of outputs that correspond to a given set of inputs (for example, bounded perturbations of a nominal input). However, many use cases of neural network verification require solving the inverse problem, or over-approximating the set of inputs that lead to certain outputs. We present the INVPROP algorithm for verifying properties over the preimage of a linearly constrained output set, which can be combined with branch-and-bound to increase precision. Contrary to other approaches, our efficient algorithm is GPU-accelerated and does not require a linear programming solver. We demonstrate our algorithm for identifying safe control regions for a dynamical system via backward reachability analysis, verifying adversarial robustness, and detecting out-of-distribution inputs to a neural network. Our results show that in certain settings, we find over-approximations over 2500x tighter than prior work while being 2.5x faster. By strengthening robustness verification with output constraints, we consistently verify more properties than the previous state-of-the-art on multiple benchmarks, including a large model with 167k neurons in VNN-COMP 2023. Our algorithm has been incorporated into the $\alpha,\!\beta$-CROWN verifier, available at https://abcrown.org.
翻译:暂无翻译