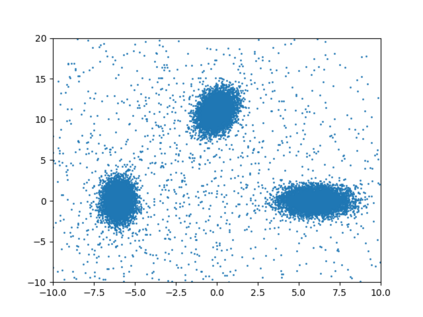
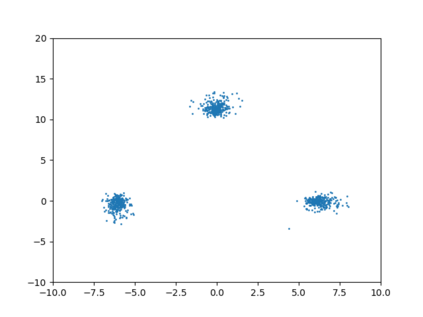
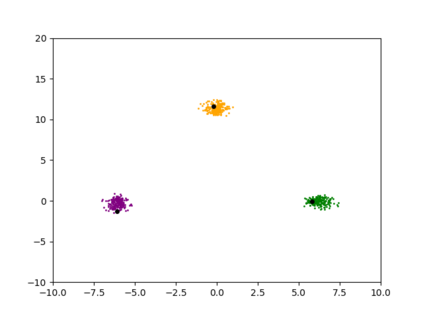
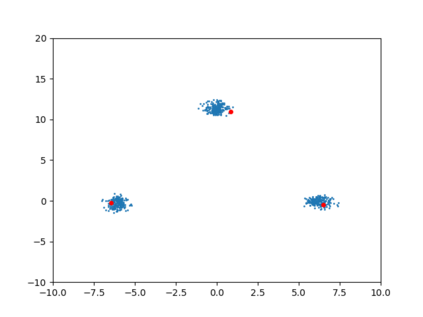
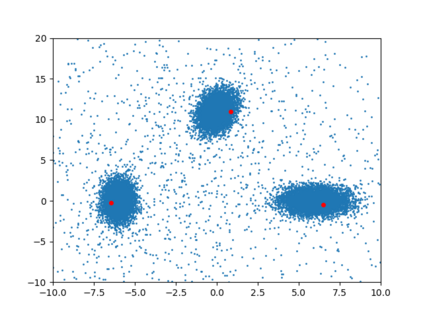
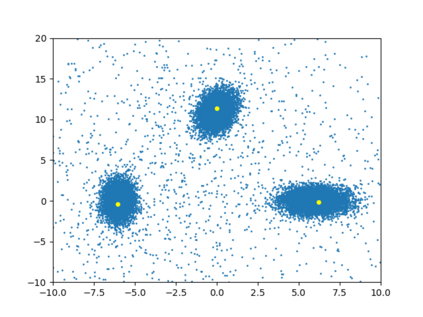
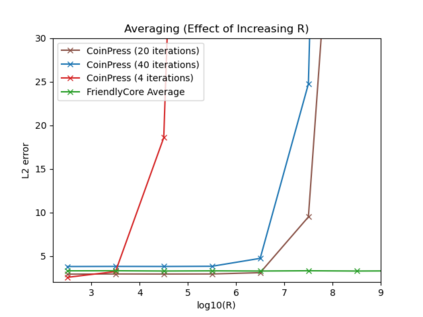
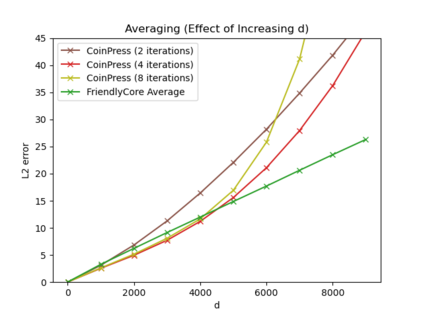
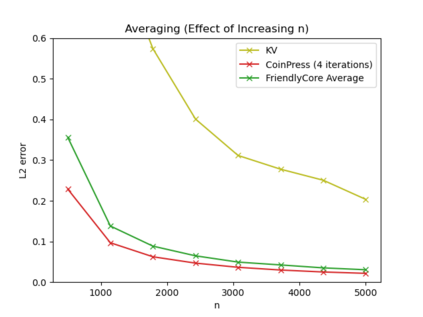
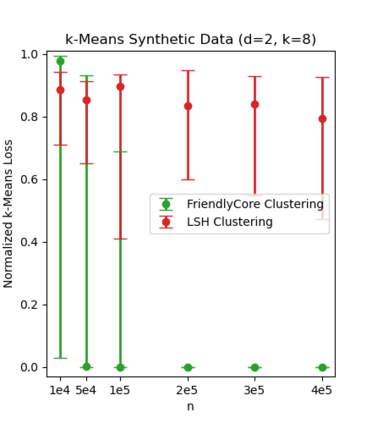
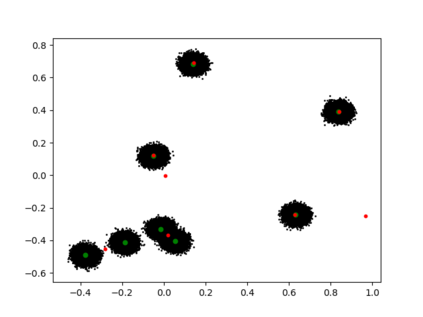
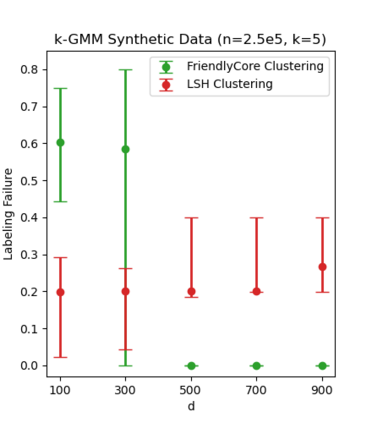
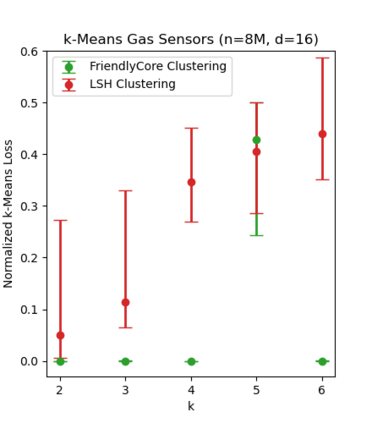
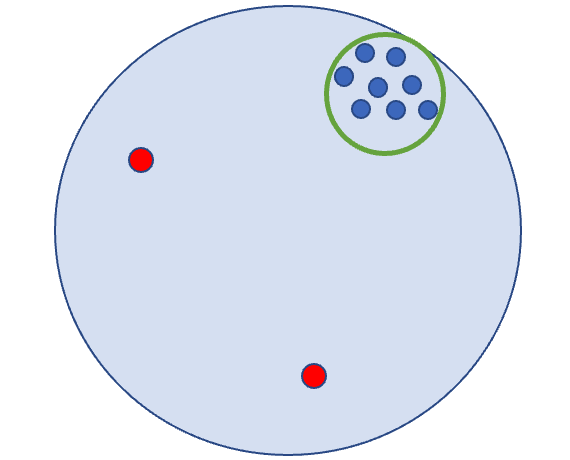
Differentially private algorithms for common metric aggregation tasks, such as clustering or averaging, often have limited practicality due to their complexity or a large number of data points that is required for accurate results. We propose a simple and practical tool, $\mathsf{FriendlyCore}$, that takes a set of points ${\cal D}$ from an unrestricted (pseudo) metric space as input. When ${\cal D}$ has effective diameter $r$, $\mathsf{FriendlyCore}$ returns a ``stable'' subset ${\cal C} \subseteq {\cal D}$ that includes all points, except possibly few outliers, and is {\em certified} to have diameter $r$. $\mathsf{FriendlyCore}$ can be used to preprocess the input before privately aggregating it, potentially simplifying the aggregation or boosting its accuracy. Surprisingly, $\mathsf{FriendlyCore}$ is light-weight with no dependence on the dimension. We empirically demonstrate its advantages in boosting the accuracy of mean estimation and clustering tasks such as $k$-means and $k$-GMM, outperforming tailored methods.
翻译:用于通用集成任务(如集成或平均)的不同私人算法通常因复杂性或准确结果所需的大量数据点而具有有限的实用性。 我们提出了一个简单实用的工具, $\ mathsf{ff}FfriendlyCore}$, 从一个不受限制的( 假的) 公用空间中取出一组点 $_cal D} 作为输入。 当$\ calD} 具有有效的直径美元时, $\ mathsf{FriendlyCore} $ 返回一个“ able” 子子 $ ball C}\ subseqeq {cal D} $, 包括所有点, 可能只有很少的外端点, 并且已经认证 $ 。 $\ mathesf{freadlyCore} 可以用来在私人集成之前预先处理输入, 有可能简化集成或提升其准确性。 令人惊讶的是, $\mathfs{f{flyCre} $ 返回一个小的重量, 和不依赖这个维度。 我们实验性地展示了它的精确性地展示了它作为GMM的精度。