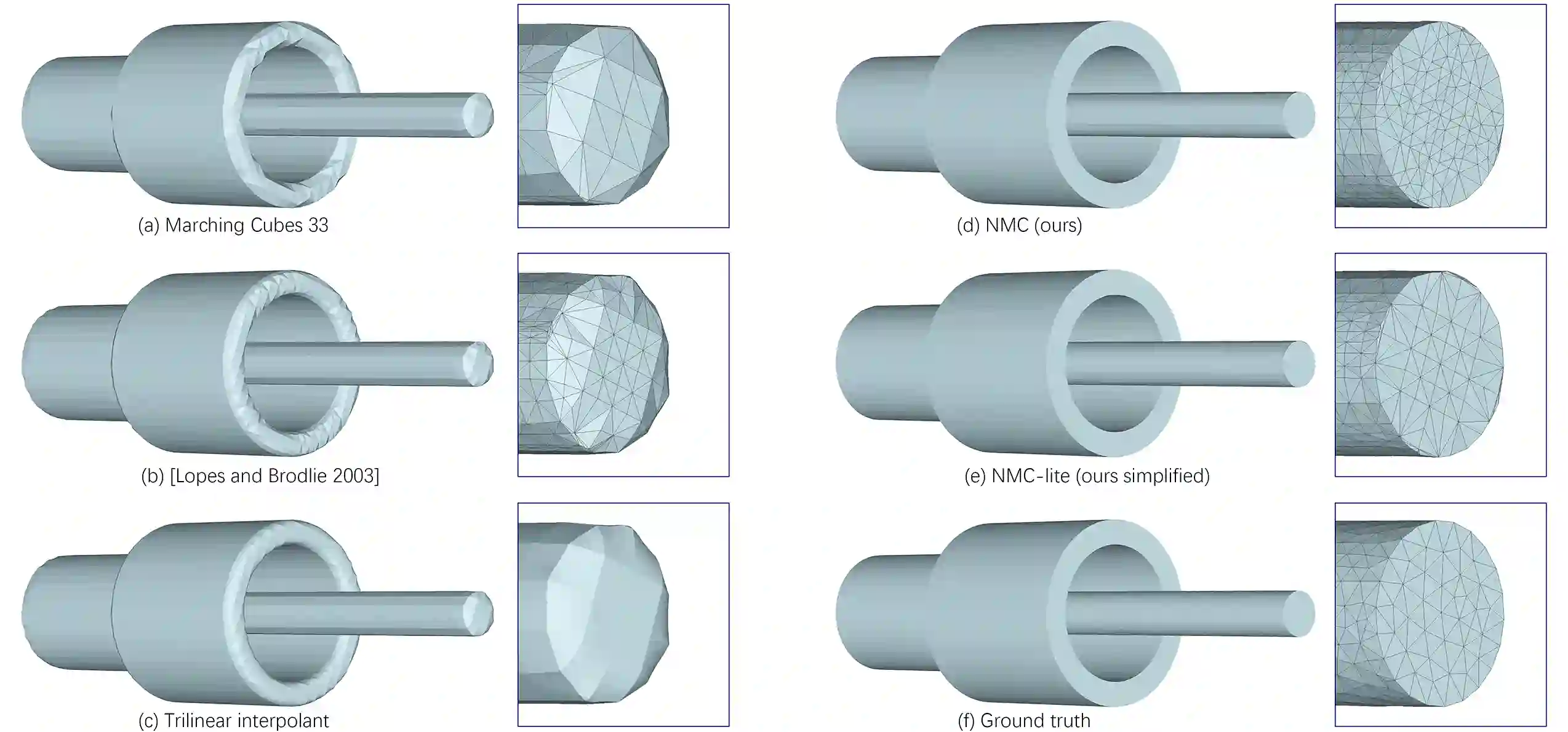
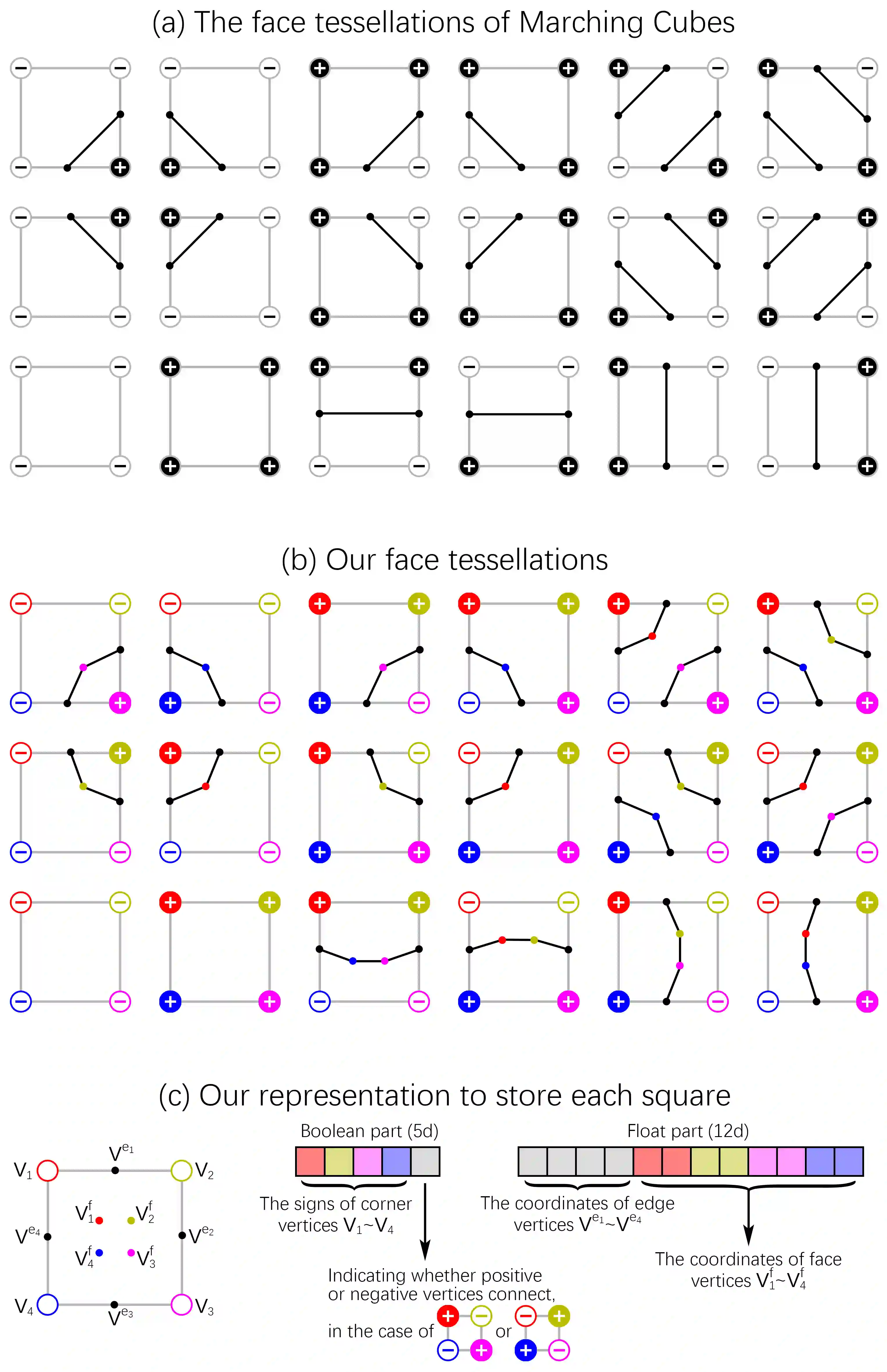
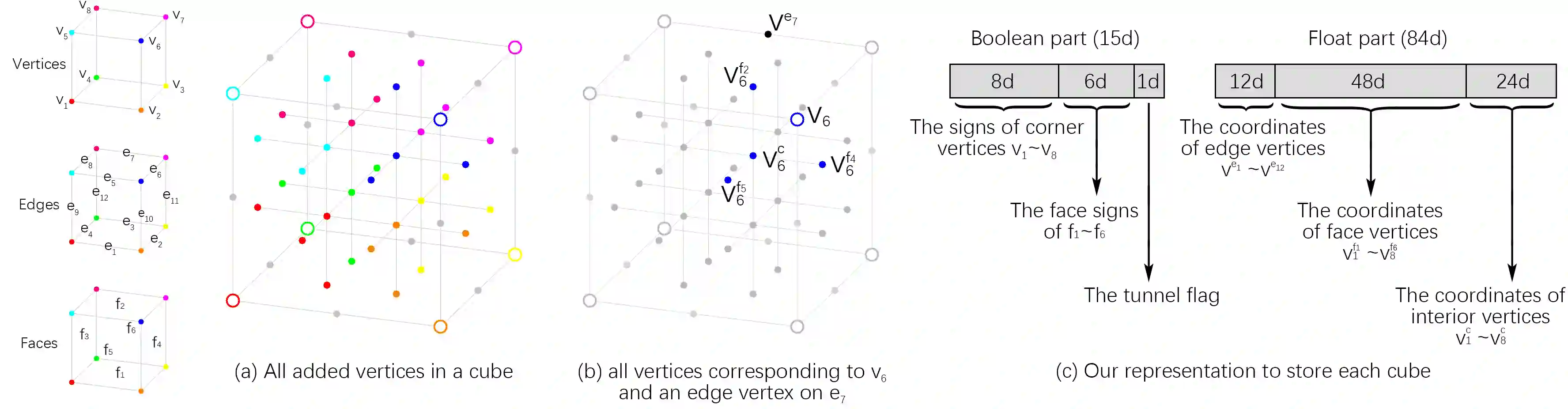
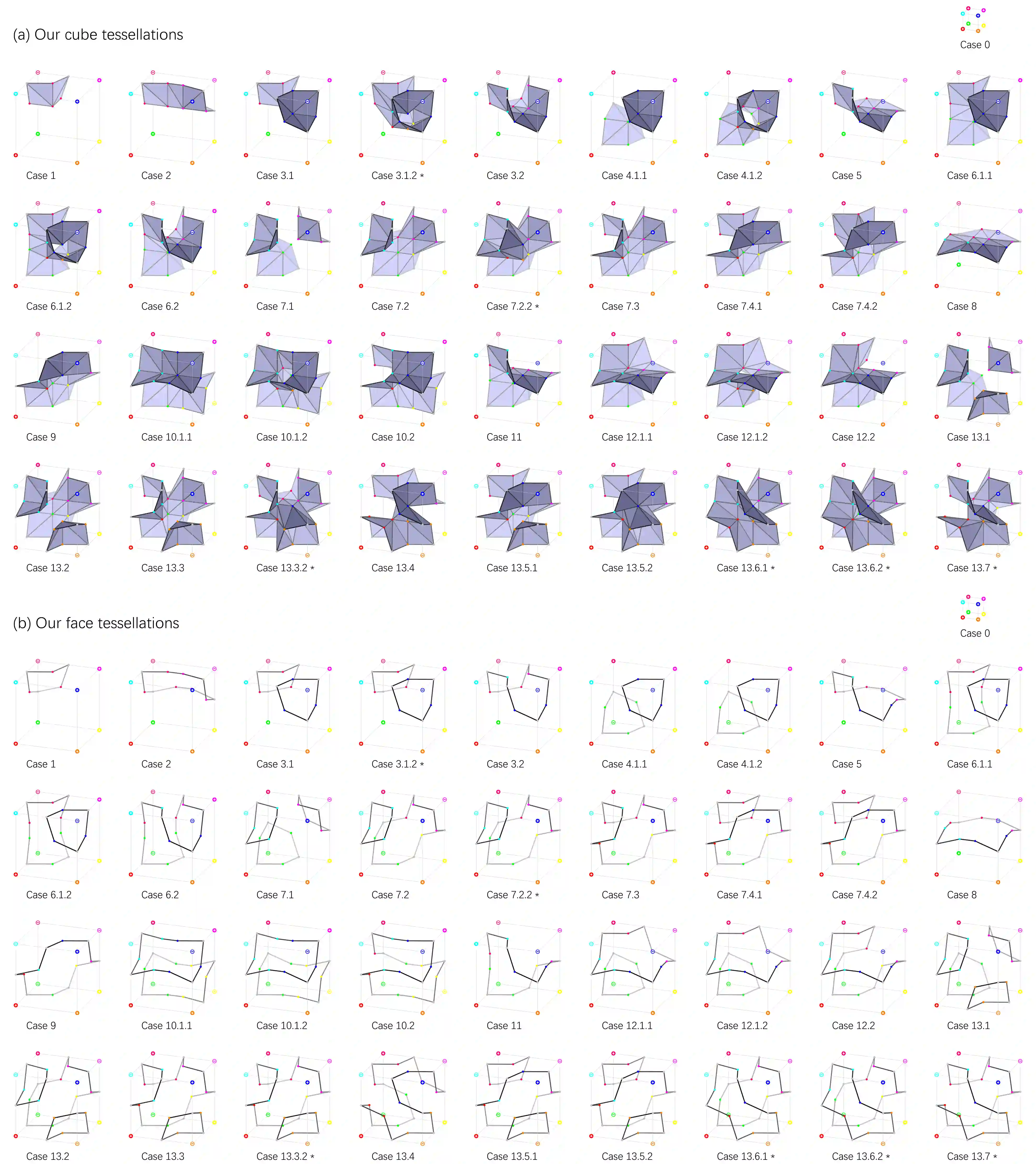
We introduce Neural Marching Cubes (NMC), a data-driven approach for extracting a triangle mesh from a discretized implicit field. Classical MC is defined by coarse tessellation templates isolated to individual cubes. While more refined tessellations have been proposed, they all make heuristic assumptions, such as trilinearity, when determining the vertex positions and local mesh topologies in each cube. In principle, none of these approaches can reconstruct geometric features that reveal coherence or dependencies between nearby cubes (e.g., a sharp edge), as such information is unaccounted for, resulting in poor estimates of the true underlying implicit field. To tackle these challenges, we re-cast MC from a deep learning perspective, by designing tessellation templates more apt at preserving geometric features, and learning the vertex positions and mesh topologies from training meshes, to account for contextual information from nearby cubes. We develop a compact per-cube parameterization to represent the output triangle mesh, while being compatible with neural processing, so that a simple 3D convolutional network can be employed for the training. We show that all topological cases in each cube that are applicable to our design can be easily derived using our representation, and the resulting tessellations can also be obtained naturally and efficiently by following a few design guidelines. In addition, our network learns local features with limited receptive fields, hence it generalizes well to new shapes and new datasets. We evaluate our neural MC approach by quantitative and qualitative comparisons to all well-known MC variants. In particular, we demonstrate the ability of our network to recover sharp features such as edges and corners, a long-standing issue of MC and its variants. Our network also reconstructs local mesh topologies more accurately than previous approaches.
翻译:我们引入了神经进化立方体( NMC), 这是一种由数据驱动的方法, 用来从离散的隐含字段中提取三角网格。 经典的MC 定义是由单个立方分离的粗糙的星系模板来定义的。 虽然提出了更精细的星系模型, 但它们在确定每个立方体的顶端位置和本地网形表层时, 都做出了更精细的假设。 原则上, 这些方法都无法重建显示附近立方体( 例如, 锐利的边缘) 之间一致性或依赖性的几何方位特征, 因为此类信息下落不明, 导致对真实的内隐含字段的直径直度估算不力。 为了应对这些挑战, 我们从深层学习的角度重新刻画MC, 设计更精细的螺旋型模板, 以及从训练 meshe 中学习螺旋位置和网形表表, 来算上的背景信息。 我们开发了一个最清楚的每立方位模型, 通过神经的处理来代表输出三角形的直径直径直径直径直径直径的内径直径直径直径直径直径直径直径直径,, 直径直径的网络结构的网络也能够显示我们用来进行着的流的网络图的网络, 。