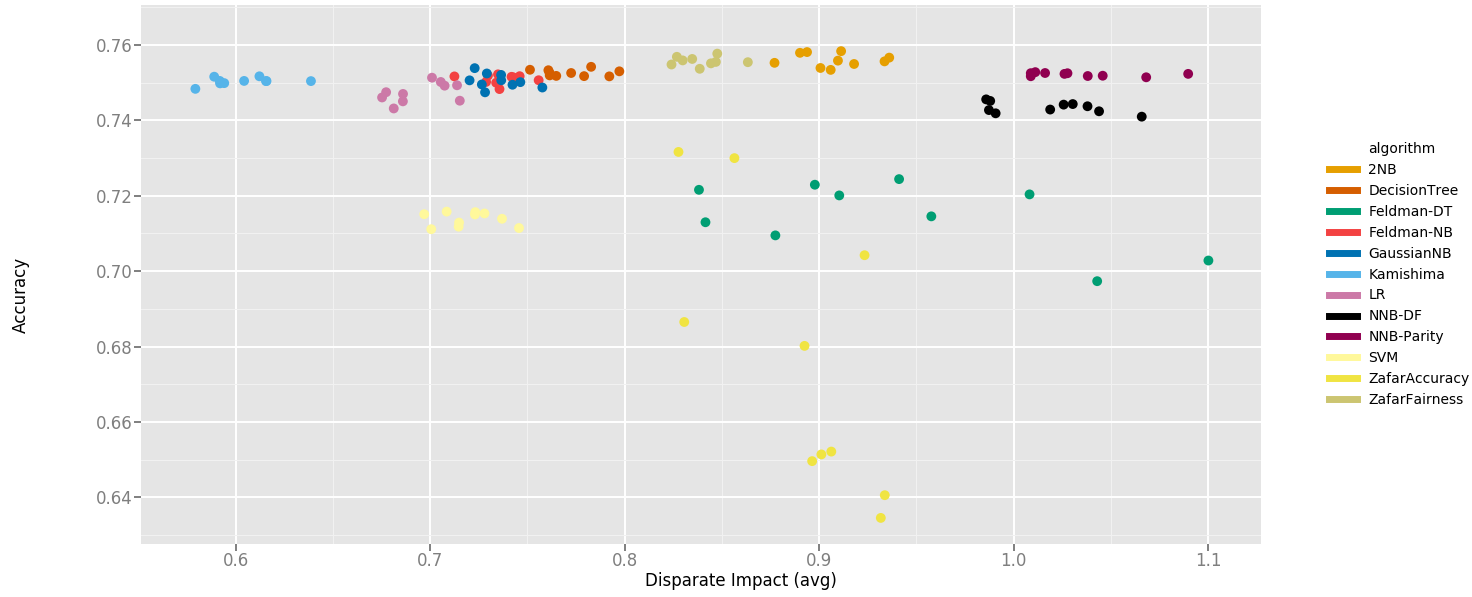
Fairness-Aware Naive Bayes Classifier for Data with Multiple Sensitive Features

Fairness-aware machine learning seeks to maximise utility in generating predictions while avoiding unfair discrimination based on sensitive attributes such as race, sex, religion, etc. An important line of work in this field is enforcing fairness during the training step of a classifier. A simple yet effective binary classification algorithm that follows this strategy is two-naive-Bayes (2NB), which enforces statistical parity - requiring that the groups comprising the dataset receive positive labels with the same likelihood. In this paper, we generalise this algorithm into N-naive-Bayes (NNB) to eliminate the simplification of assuming only two sensitive groups in the data and instead apply it to an arbitrary number of groups. We propose an extension of the original algorithm's statistical parity constraint and the post-processing routine that enforces statistical independence of the label and the single sensitive attribute. Then, we investigate its application on data with multiple sensitive features and propose a new constraint and post-processing routine to enforce differential fairness, an extension of established group-fairness constraints focused on intersectionalities. We empirically demonstrate the effectiveness of the NNB algorithm on US Census datasets and compare its accuracy and debiasing performance, as measured by disparate impact and DF-$\epsilon$ score, with similar group-fairness algorithms. Finally, we lay out important considerations users should be aware of before incorporating this algorithm into their application, and direct them to further reading on the pros, cons, and ethical implications of using statistical parity as a fairness criterion.