Games and Computational Complexity

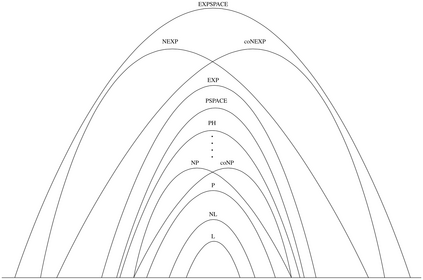
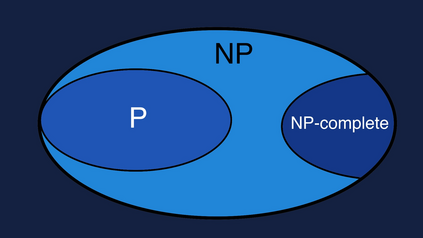
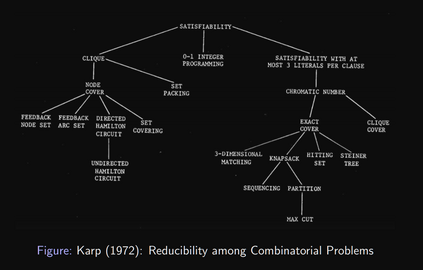
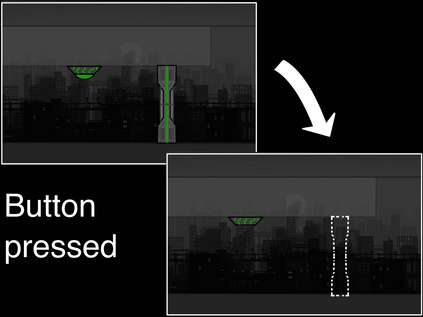
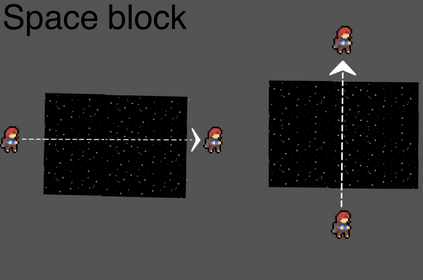
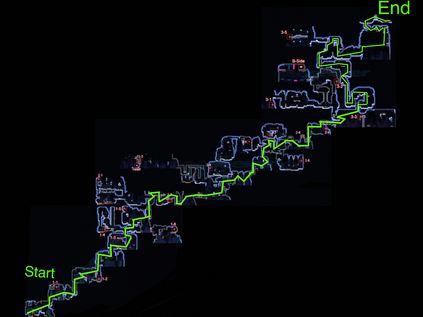
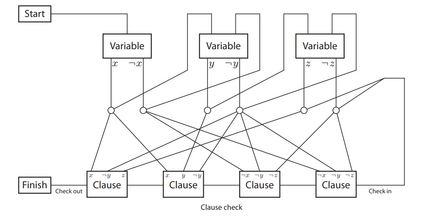
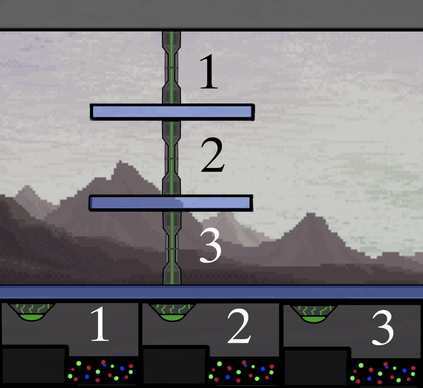
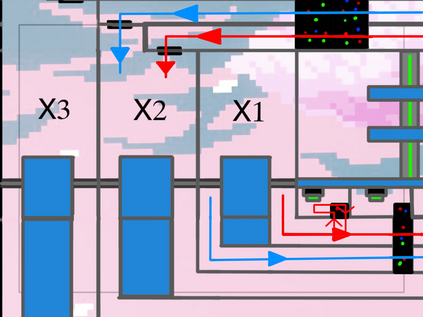
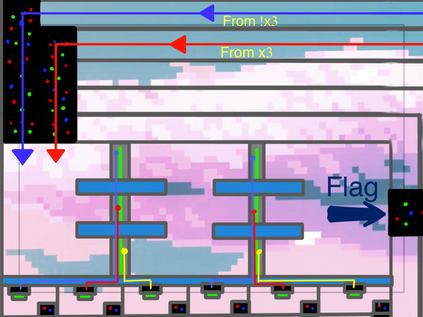
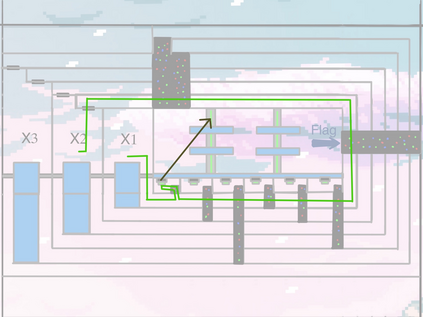
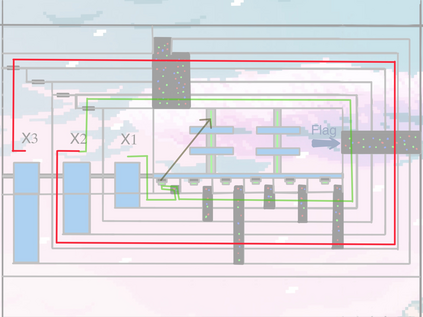
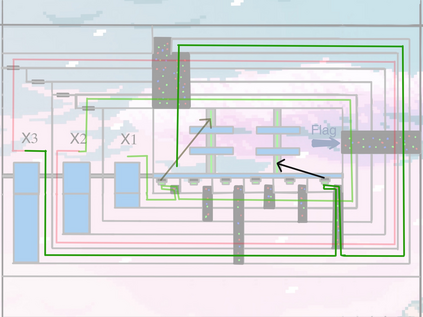
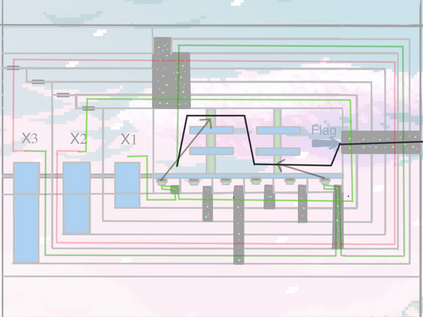
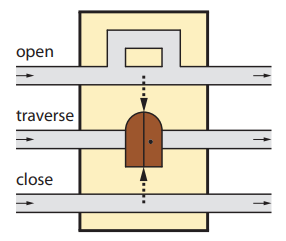
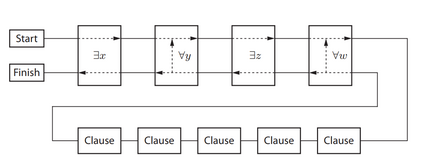
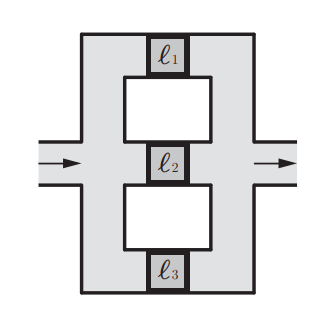
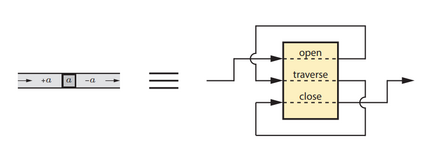
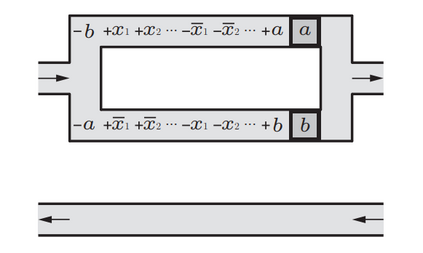
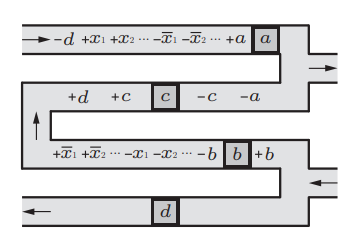
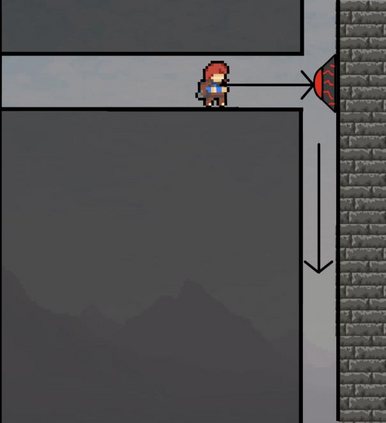
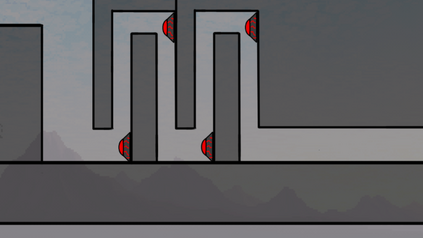
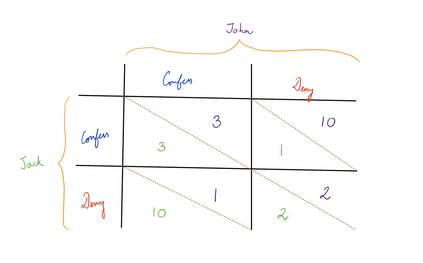
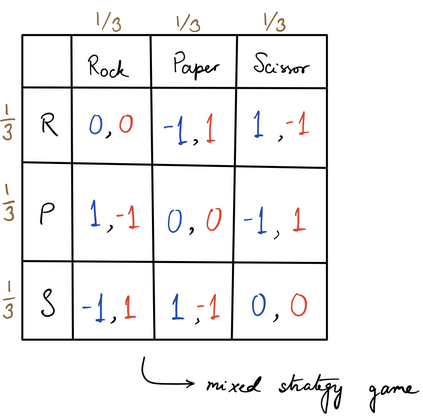
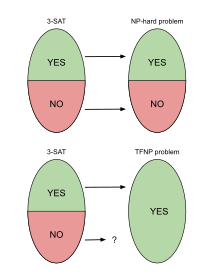
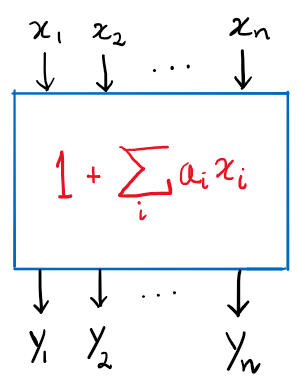
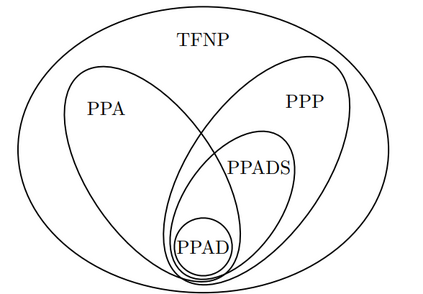
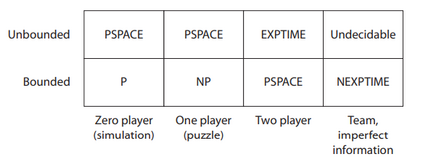
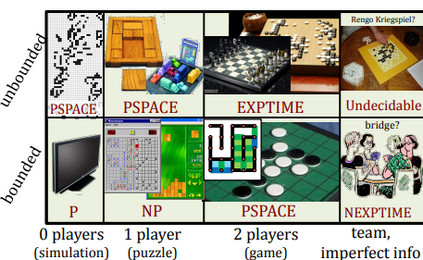
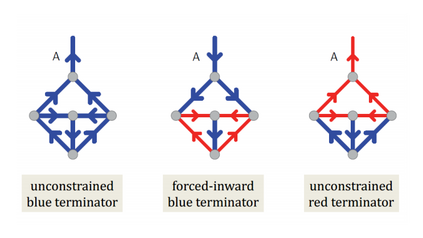
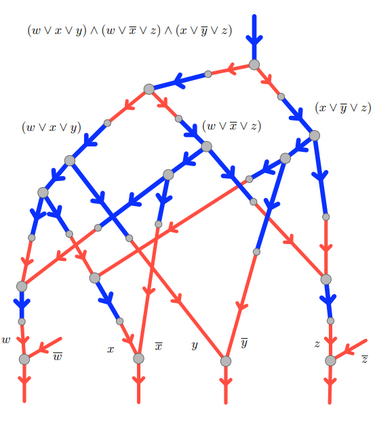
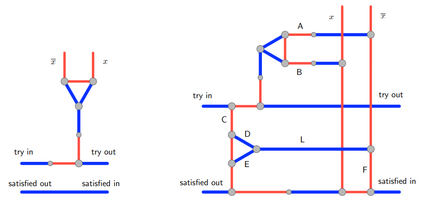
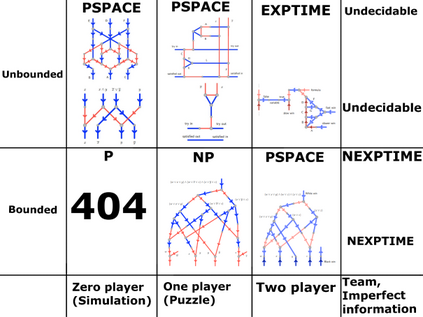
Computers can solve a wide spectrum of problems, but they can't solve all the problems, some problems can never have a solution, some problems can be, but they require more space the size of the universe, or more time than the age of the universe on our computational models. So how do we measure such aspects of a problem? We do that using Complexity Theory, which deals with how and why a problem is harder than a different problem, and how to classify problems based on the resources they require. Do Protein folding and Sudoku have something in common? It might not seem so but Complexity Theory tells us that if we had an algorithm that could solve Sudoku efficiently then we could adapt it to predict for protein folding. This same property is held by classic platformer games such as Super Mario Bros, which was proven to be NP-complete by Erik Demaine et. al. Here, we shall prove how the game "Celeste" also shares such property by proving it to be NP-complete and then later show how a small change in it makes the game presumably harder to compute - to be precise, PSPACE-complete. We also present several formalisms related to modelling of games in general and 2D platformer video games in general. In the end we also present a compilation of generalized meta-theorems originally formulated by Giovanni Viglietta.