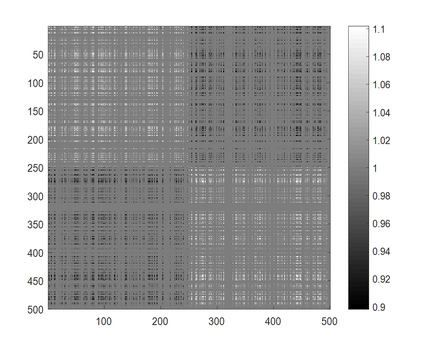
In this paper, we propose a data-adaptive non-parametric kernel learning framework in margin based kernel methods. In model formulation, given an initial kernel matrix, a data-adaptive matrix with two constraints is imposed in an entry-wise scheme. Learning this data-adaptive matrix in a formulation-free strategy enlarges the margin between classes and thus improves the model flexibility. The introduced two constraints are imposed either exactly (on small data sets) or approximately (on large data sets) in our model, which provides a controllable trade-off between model flexibility and complexity with theoretical demonstration. In algorithm optimization, the objective function of our learning framework is proven to be gradient-Lipschitz continuous. Thereby, kernel and classifier/regressor learning can be efficiently optimized in a unified framework via Nesterov's acceleration. For the scalability issue, we study a decomposition-based approach to our model in the large sample case. The effectiveness of this approximation is illustrated by both empirical studies and theoretical guarantees. Experimental results on various classification and regression benchmark data sets demonstrate that our non-parametric kernel learning framework achieves good performance when compared with other representative kernel learning based algorithms.
翻译:在本文中,我们提出一个基于边心法的数据适应性非参数内核学习框架; 在模型拟订中,给最初的内核矩阵提供初步的内核矩阵,对初始的内核矩阵实行数据适应性矩阵,对初始的内核计划实行两种限制; 在不制定战略中学习这一数据适应性矩阵,扩大了阶级之间的距离,从而改进了模型的灵活性; 引入了两种限制,要么是完全(小数据集),要么是(大数据集)在我们模型中强加的,这提供了模型灵活性和复杂性与理论示范之间的可控制的权衡取舍; 在算法优化中,我们的学习框架的客观功能被证明是梯度-里普施茨的连续的。 由此,内核和分类/递归学可以在一个统一的框架中,通过Nessterov的加速来有效地优化。 关于可缩放问题,我们研究了在大型抽样案中对我们模型的一种基于分解的方位方法。 这种近似值的效力通过实证研究和理论保证加以说明。