Analysis of obstacles immersed in viscous fluids using Brinkman's law for steady Stokes and Navier-Stokes equations

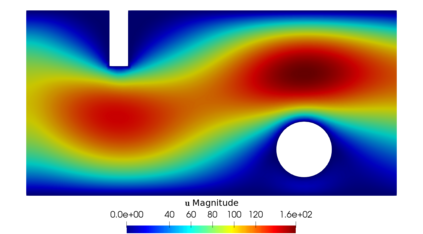
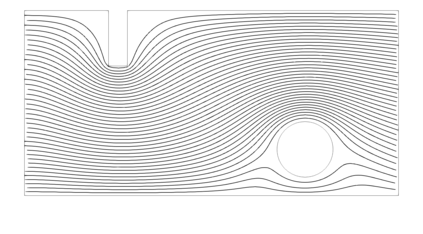
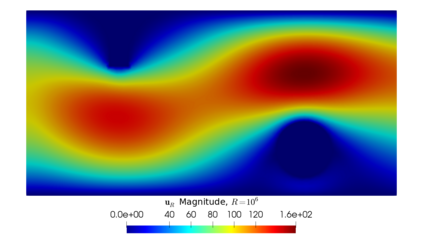
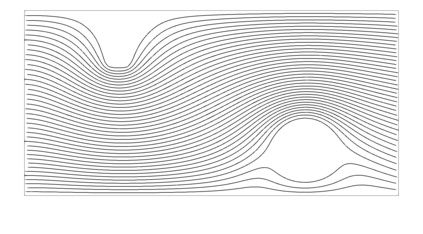
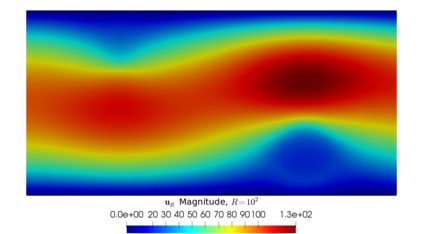
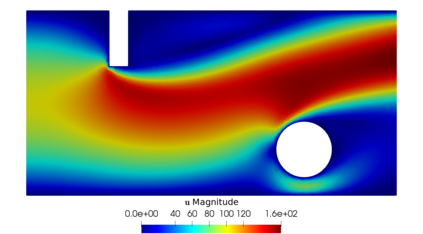
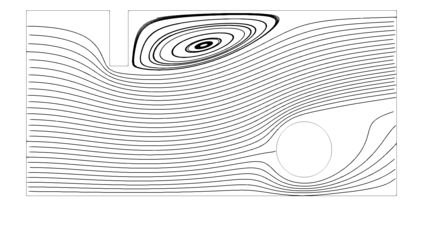
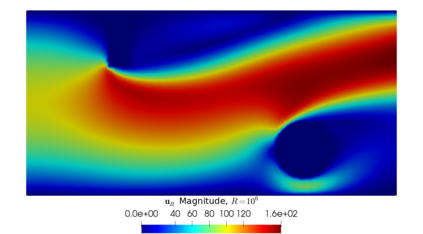
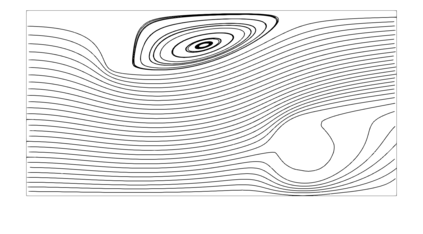
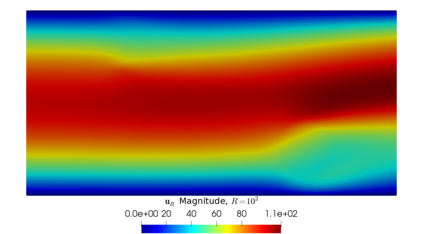
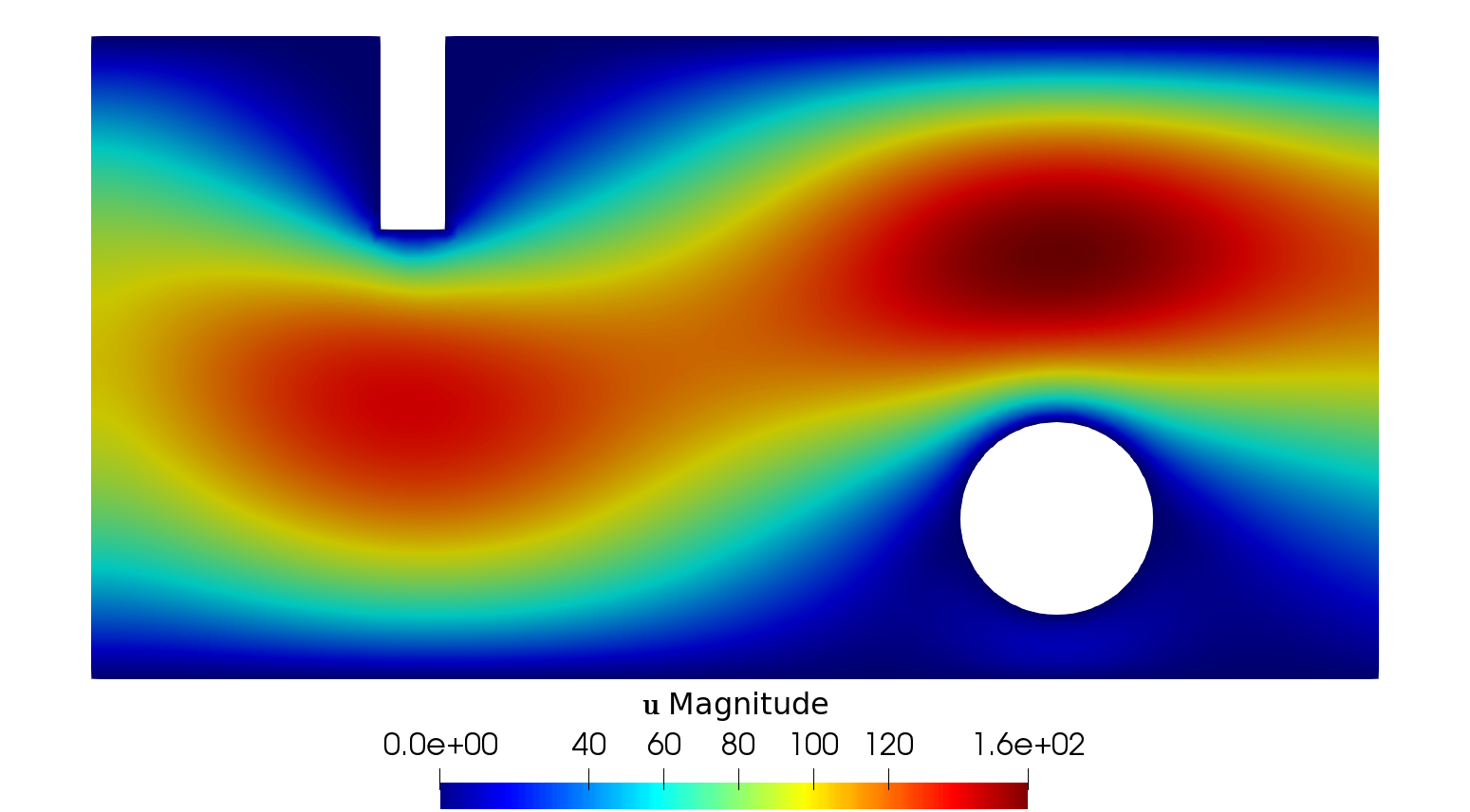
From the steady Stokes and Navier-Stokes models, a penalization method has been considered by several authors for approximating those fluid equations around obstacles. In this work, we present a justification for using fictitious domains to study obstacles immersed in incompressible viscous fluids through a simplified version of Brinkman's law for porous media. If the scalar function $\psi$ is considered as the inverse of permeability, it is possible to study the singularities of $\psi$ as approximations of obstacles (when $\psi$ tends to $\infty$) or of the domain corresponding to the fluid (when $\psi = 0$ or is very close to $0$). The strong convergence of the solution of the perturbed problem to the solution of the strong problem is studied, also considering error estimates that depend on the penalty parameter, both for fluids modeled with the Stokes and Navier-Stokes equations with inhomogeneous boundary conditions. A numerical experiment is presented that validates this result and allows to study the application of this perturbed problem simulation of flows and the identification of obstacles.