Bound-Preserving Finite-Volume Schemes for Systems of Continuity Equations with Saturation

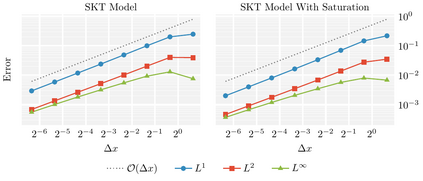
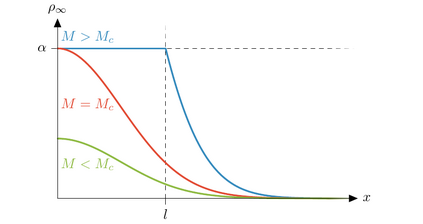
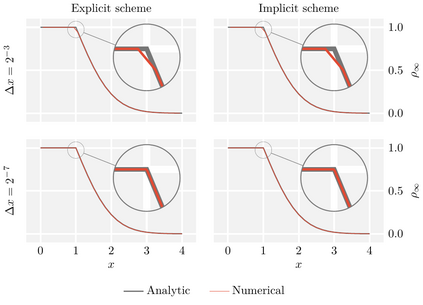
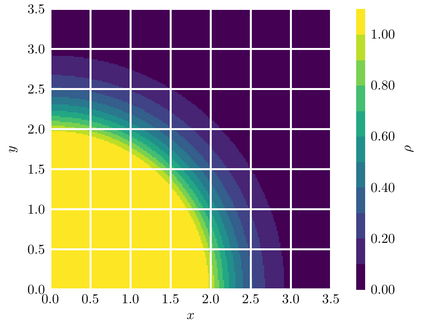
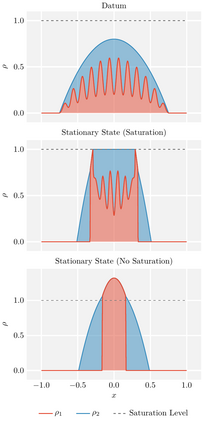
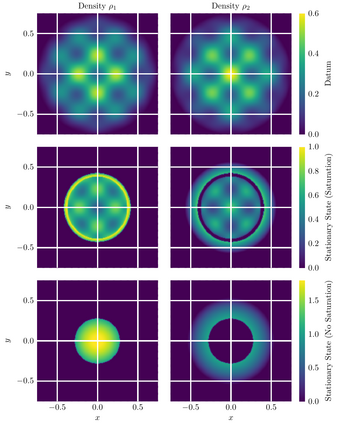
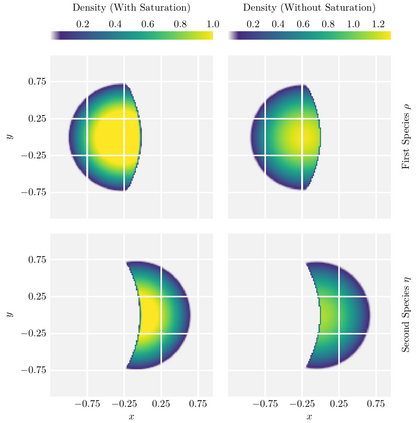
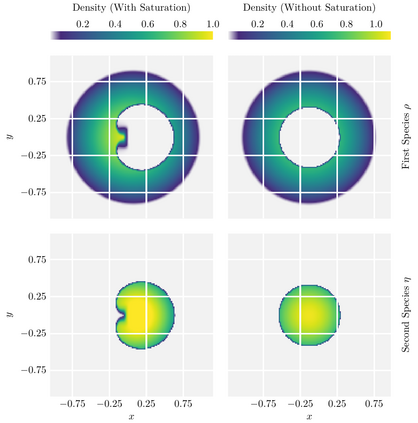
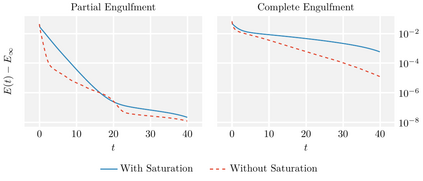
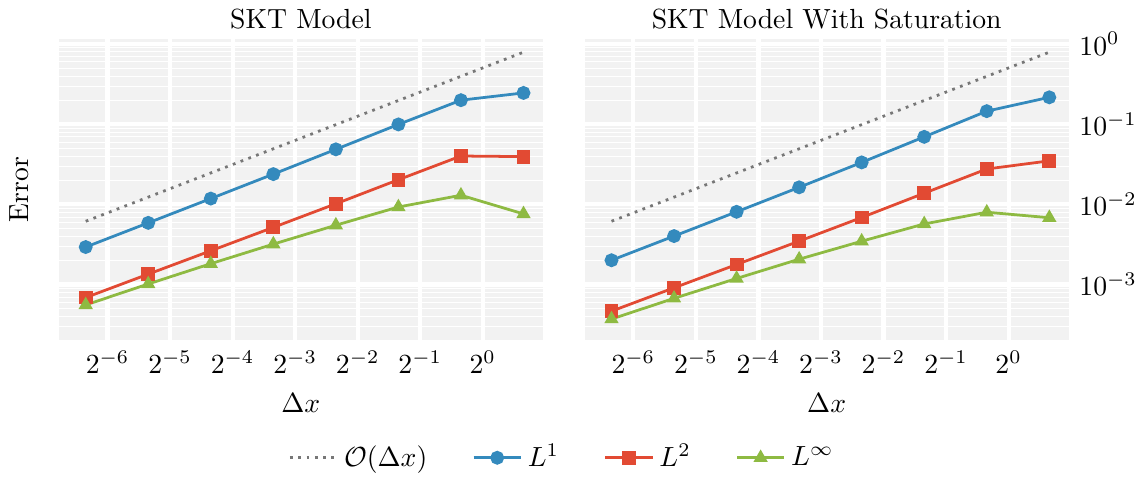
We propose finite-volume schemes for general continuity equations which preserve positivity and global bounds that arise from saturation effects in the mobility function. In the particular case of gradient flows, the schemes dissipate the free energy at the fully discrete level. Moreover, these schemes are generalised to coupled systems of non-linear continuity equations, such as multispecies models in mathematical physics or biology, preserving the bounds and the dissipation of the energy whenever applicable. These results are illustrated through extensive numerical simulations which explore known behaviours in biology and showcase new phenomena not yet described by the literature.