From omnitigs to macrotigs: a linear-time algorithm for safe walks -- common to all closed arc-coverings of a directed graph

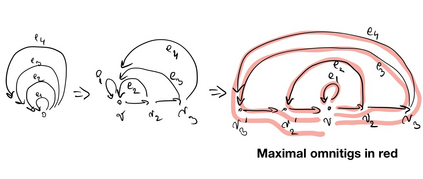
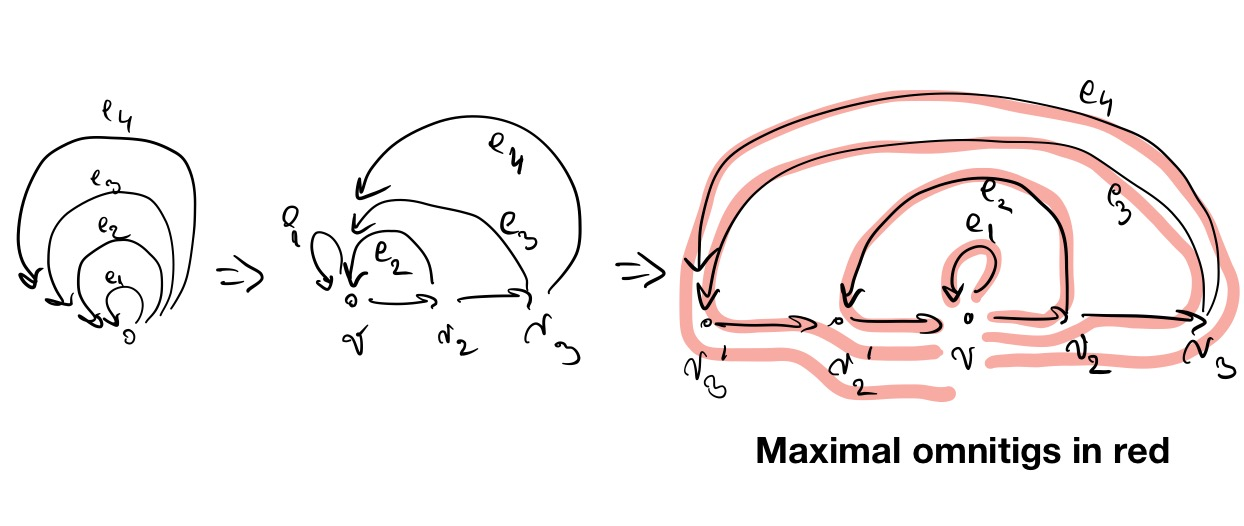
A partial solution to a problem is called safe if it appears in all solutions to the problem. Motivated by the genome assembly problem in bioinformatics, Tomescu and Medvedev (RECOMB 2016) posed the question of finding the safe walks present in all closed arc-covering walks, and gave a characterization of them (omnitigs). An $O(nm)$-time algorithm enumerating all maximal omnitigs on a directed graph with $n$ nodes and $m$ arcs was given by Cairo et al. (ACM Trans. Algorithms 2019), along with a family of graphs where the total length of maximal omnitigs is $\Theta(nm)$. In this paper we describe an $O(m)$-time algorithm to identify all maximal omnitigs, thanks to the discovery of a family of walks (macrotigs) with the property that all the non-trivial omnitigs are univocal extensions of subwalks of a macrotig. This has several consequences: (i) A linear output-sensitive algorithm enumerating all maximal omnitigs, that avoids to pay $\Theta(nm)$ when the output is smaller, whose existence was open. (ii) A compact representation of all maximal omnitigs, which allows, e.g., for $O(m)$-time computation of various statistics on them. (iii) A powerful tool for finding safe walks for related covering problems.