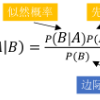
For classification tasks, probabilistic models can be categorized into two disjoint classes: generative or discriminative. It depends on the posterior probability computation of the label $x$ given the observation $y$, $p(x | y)$. On the one hand, generative classifiers, like the Naive Bayes or the Hidden Markov Model (HMM), need the computation of the joint probability p(x,y), before using the Bayes rule to compute $p(x | y)$. On the other hand, discriminative classifiers compute $p(x | y)$ directly, regardless of the observations' law. They are intensively used nowadays, with models as Logistic Regression, Conditional Random Fields (CRF), and Artificial Neural Networks. However, the recent Entropic Forward-Backward algorithm shows that the HMM, considered as a generative model, can also match the discriminative one's definition. This example leads to question if it is the case for other generative models. In this paper, we show that the Naive Bayes classifier can also match the discriminative classifier definition, so it can be used in either a generative or a discriminative way. Moreover, this observation also discusses the notion of Generative-Discriminative pairs, linking, for example, Naive Bayes and Logistic Regression, or HMM and CRF. Related to this point, we show that the Logistic Regression can be viewed as a particular case of the Naive Bayes used in a discriminative way.
翻译:对于分类任务,概率模型可以分为两种不相干类别:基因化或歧视性。 它取决于根据观察值美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元。 一方面, 基因分类器, 如Nive Bayes 或隐藏 Markov 模型( HMM ), 需要计算共同概率 p (x,y), 然后再使用 Bay 规则来计算 $p (x ) y( y) 。 另一方面, 歧视性分类器直接计算 $p (x y) 美元, 不论观察法如何。 它们现在被大量使用, 模型是物流递增、 调随机字段( CRF) 和人工神经网络。 然而, 最近的 Entropic pregard- Backward 算法显示, 作为一种归正模型, HMM, 也可以与歧视性定义相匹配。, 这个示例是, 也就是它与其他归正alive Bayeralalalisional 或变正性 解释性 方法, 用来解释性 。