Simulation of crack propagation through voxel-based, heterogeneous structures based on eigenerosion and finite cells

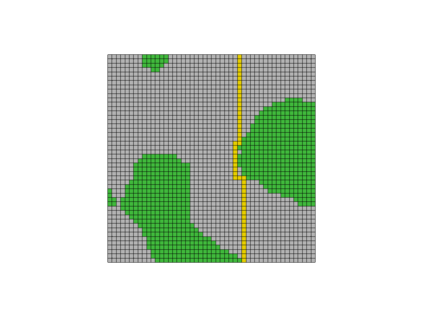
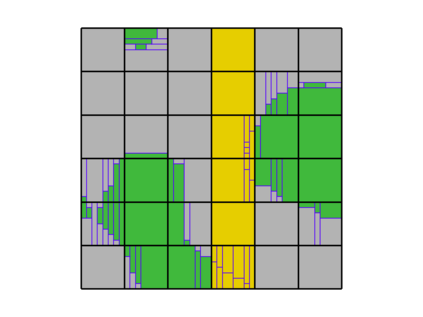
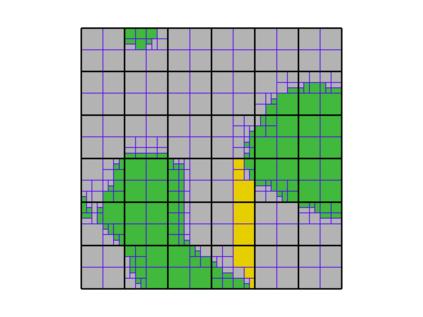
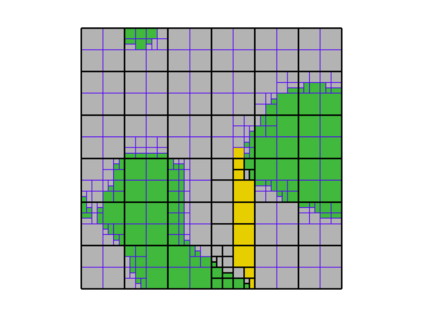
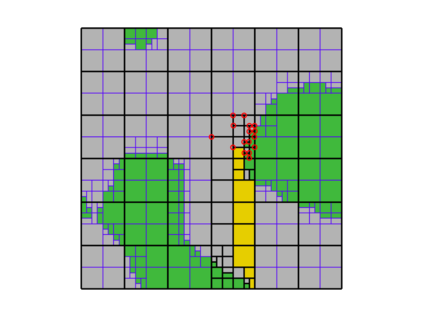
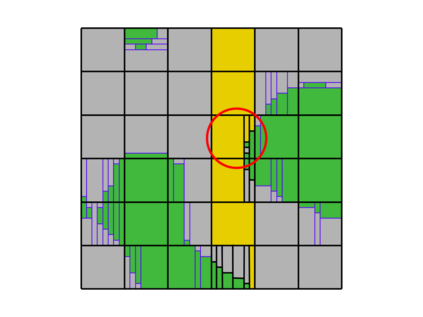
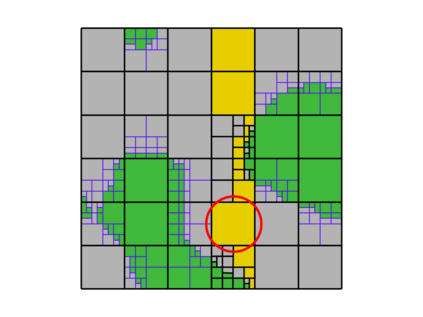
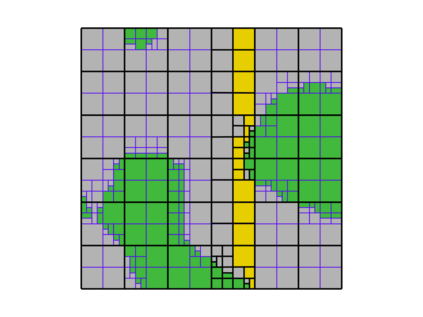
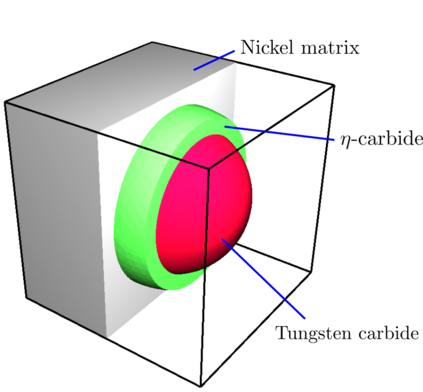
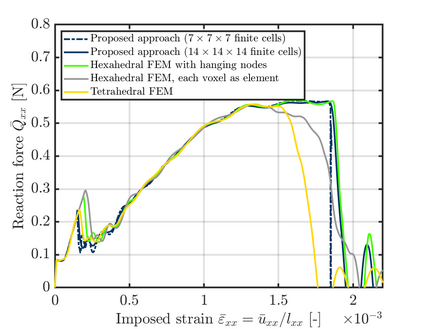
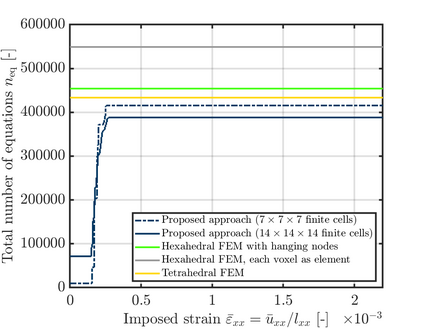
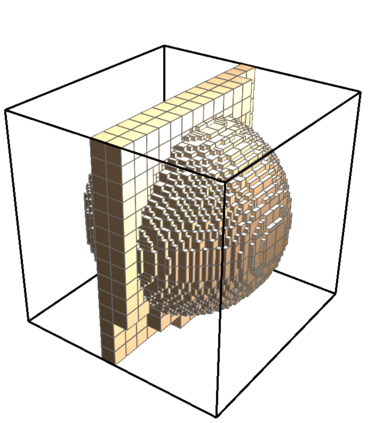
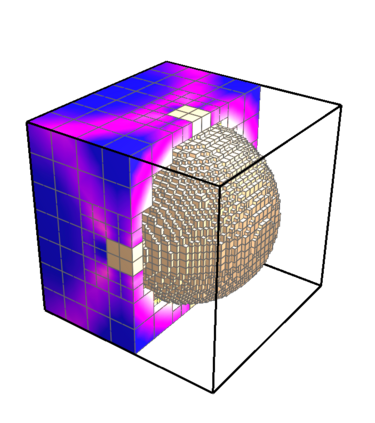
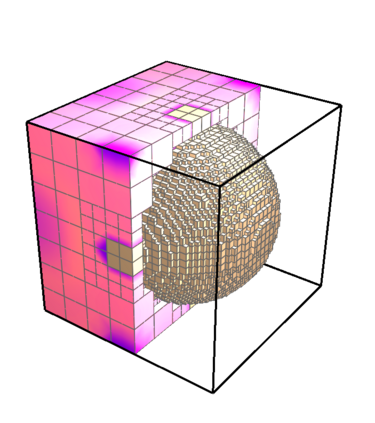
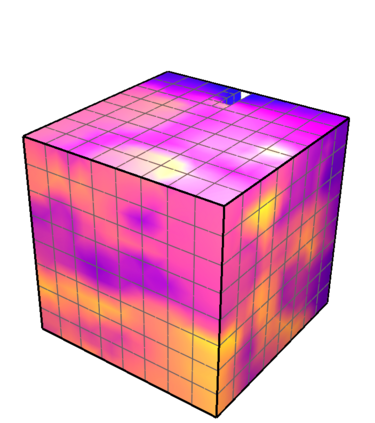
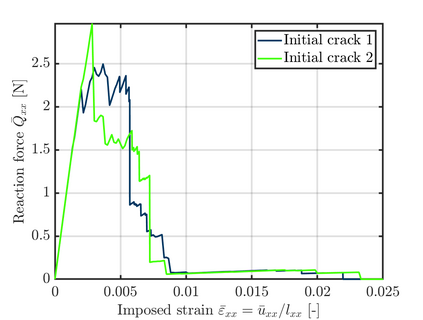
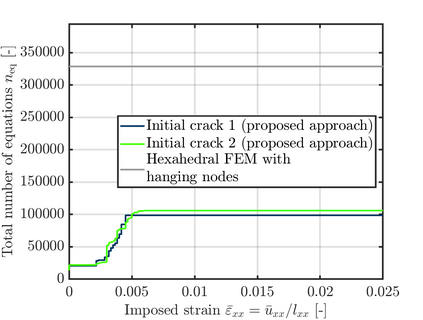
This paper presents an algorithm for the efficient simulation of ductile crack propagation through heterogeneous structures, as e.g. metallic microstructures, which are given as voxel data. These kinds of simulations are required for e.g., the numerical investigation of wear mechanisms at small length scales, which is still a challenging task in engineering. The basic idea of the proposed algorithm is to combine the advantages of the Finite Cell Method allowing for a convenient integration of heterogeneous finite element problems with the eigenerosion approach to still enable the mesh-independent simulation of crack propagation. The major component is to switch from finite subcells to finite elements wherever the crack progresses, thereby automatically adaptively refining at the crack tip by managing the newly appearing nodes as hanging nodes. Technically relevant problems of crack propagation at the microscale are mostly linked with sub-critical crack growth where the crack moves fast and stepwise with subsequent load cycles. Therefore, inertia may become important which is why dynamics are taken into account by spreading the mass of the eroded elements to the nodes to avoid a loss in mass resulting from the erosion procedure. Furthermore, a certain treatment for the finite cell decomposition is considered in order to ensure efficiency and accuracy. The numerical framework as well as the voxel decomposition techniques are analyzed in detail in different three-dimensional numerical examples to show the performance of the proposed approach.