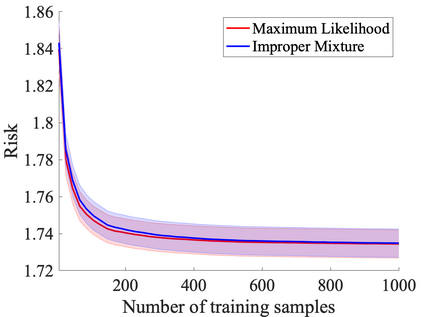
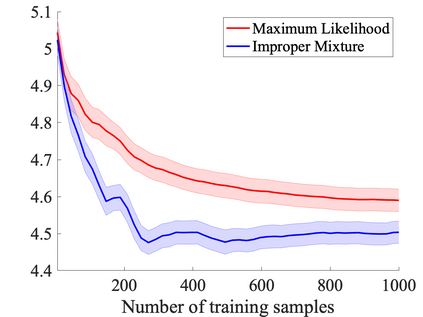
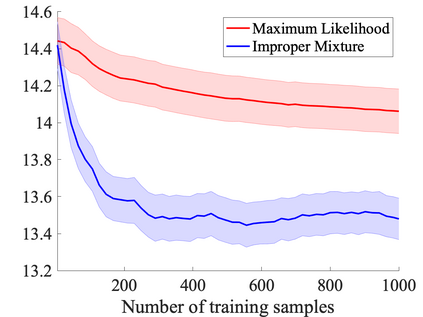
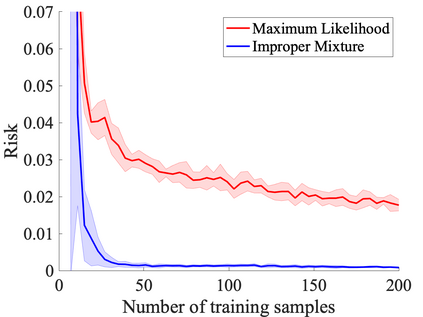
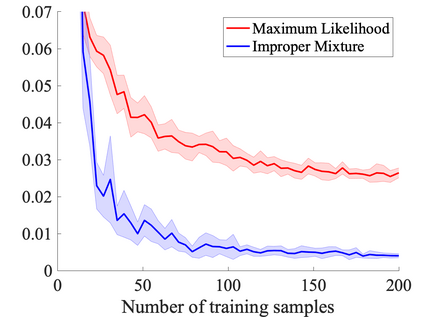
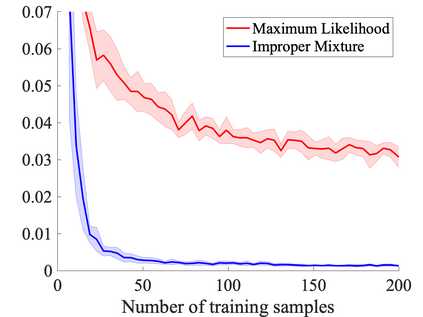
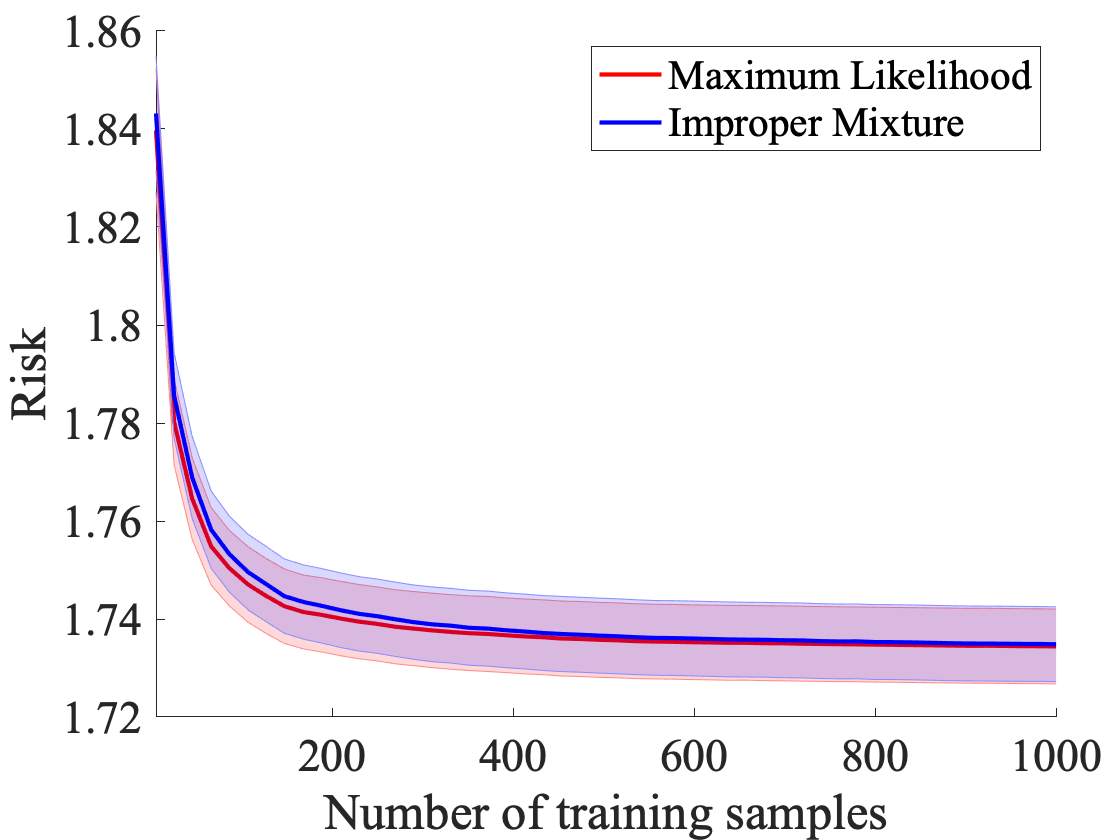
We study probabilistic prediction games when the underlying model is misspecified, investigating the consequences of predicting using an incorrect parametric model. We show that for a broad class of loss functions and parametric families of distributions, the regret of playing a "proper" predictor -- one from the putative model class -- relative to the best predictor in the same model class has lower bound scaling at least as $\sqrt{\gamma n}$, where $\gamma$ is a measure of the model misspecification to the true distribution in terms of total variation distance. In contrast, using an aggregation-based (improper) learner, one can obtain regret $d \log n$ for any underlying generating distribution, where $d$ is the dimension of the parameter; we exhibit instances in which this is unimprovable even over the family of all learners that may play distributions in the convex hull of the parametric family. These results suggest that simple strategies for aggregating multiple learners together should be more robust, and several experiments conform to this hypothesis.
翻译:当基本模型被错误地指定时,我们研究概率预测游戏,调查使用不正确的参数模型预测预测结果。我们显示,对于一个广泛的损失类别,即功能和分布的参数分界,玩“正确”预测器的遗憾 -- -- 一个来自模型类中的模型预测器 -- -- 相对于同一模型类中的最佳预测器来说,其约束性较低,至少以$=sqrt{gamma n}计算,其中$\gamma$是衡量模型在总变差距离方面与真实分布不相符的尺度的尺度。相反,使用一个基于聚合的(不正确)学习者,人们可以为任何潜在生成分布而后悔地得到$d\log n$,而美元是参数的维度;我们展示出这样的例子:即使在所有可能玩分母体船分布的学习者的家庭中,这一点是无法简化的。这些结果表明,将多个学习者集中在一起的简单策略应该更加稳健,而几个实验也符合这一假设。