{Generative Adversarial Learning of Sinkhorn Algorithm Initializations}

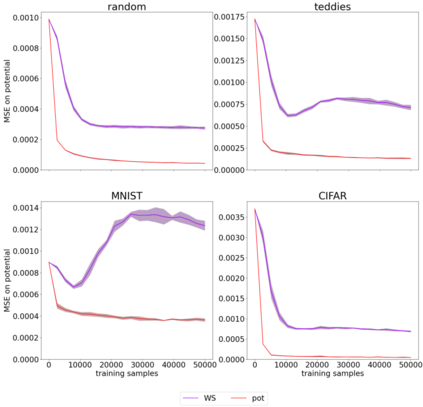
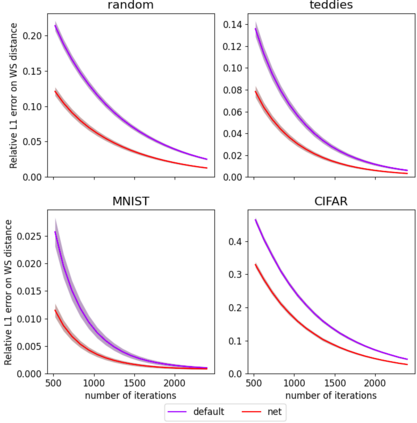
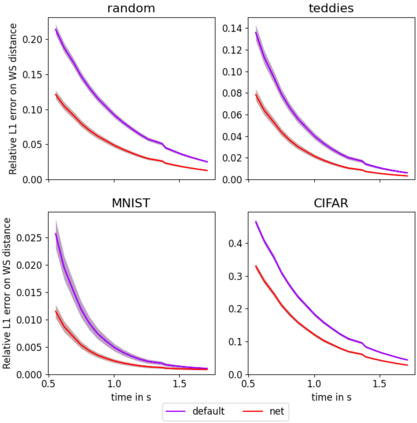
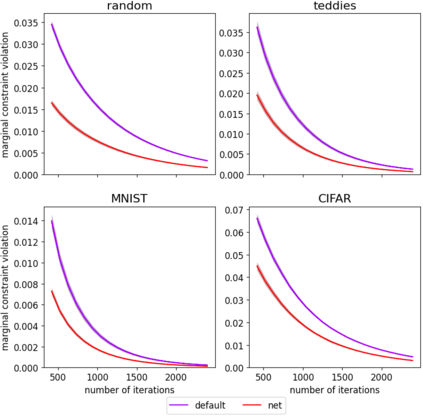
The Sinkhorn algorithm (arXiv:1306.0895) is the state-of-the-art to compute approximations of optimal transport distances between discrete probability distributions, making use of an entropically regularized formulation of the problem. The algorithm is guaranteed to converge, no matter its initialization. This lead to little attention being paid to initializing it, and simple starting vectors like the n-dimensional one-vector are common choices. We train a neural network to compute initializations for the algorithm, which significantly outperform standard initializations. The network predicts a potential of the optimal transport dual problem, where training is conducted in an adversarial fashion using a second, generating network. The network is universal in the sense that it is able to generalize to any pair of distributions of fixed dimension after training, and we prove that the generating network is universal in the sense that it is capable of producing any pair of distributions during training. Furthermore, we show that for certain applications the network can be used independently.