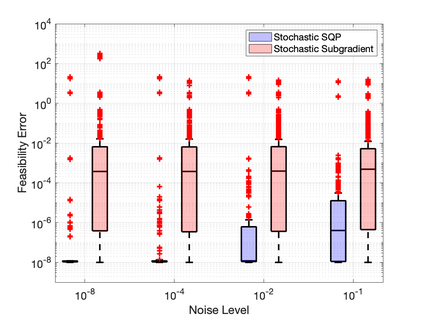
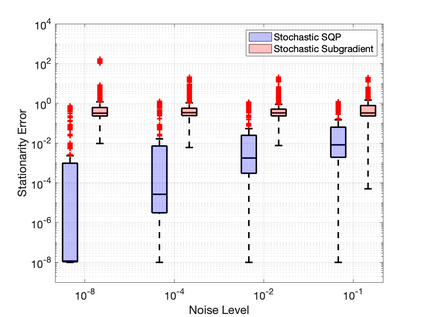
A sequential quadratic optimization algorithm is proposed for solving smooth nonlinear equality constrained optimization problems in which the objective function is defined by an expectation of a stochastic function. The algorithmic structure of the proposed method is based on a step decomposition strategy that is known in the literature to be widely effective in practice, wherein each search direction is computed as the sum of a normal step (toward linearized feasibility) and a tangential step (toward objective decrease in the null space of the constraint Jacobian). However, the proposed method is unique from others in the literature in that it both allows the use of stochastic objective gradient estimates and possesses convergence guarantees even in the setting in which the constraint Jacobians may be rank deficient. The results of numerical experiments demonstrate that the algorithm offers superior performance when compared to popular alternatives.
翻译:提出连续二次优化算法,以解决平滑的非线性平等限制优化的问题,在这种算法中,目标功能是由对随机功能的预期来界定的。拟议方法的算法结构基于文献中已知的逐步分解战略,在实践中具有广泛效力,即每个搜索方向都是以正常步骤(向线性可行性过渡)和相近步骤(向向向限制雅各雅各雅各雅各雅各雅各雅各雅各雅各雅各雅各的空空空空空间迈进)的总和来计算。然而,拟议方法与文献中的其他方法是独特的,因为它既允许使用随机客观梯度估计数,也拥有趋同保证,即使在Jacobian人的制约排位可能存在缺陷的环境下也是如此。数字实验的结果表明,与流行的替代方法相比,算法具有优异的性能。