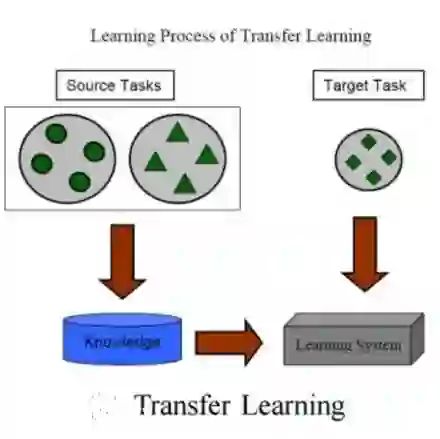
Solving differential equations efficiently and accurately sits at the heart of progress in many areas of scientific research, from classical dynamical systems to quantum mechanics. There is a surge of interest in using Physics-Informed Neural Networks (PINNs) to tackle such problems as they provide numerous benefits over traditional numerical approaches. Despite their potential benefits for solving differential equations, transfer learning has been under explored. In this study, we present a general framework for transfer learning PINNs that results in one-shot inference for linear systems of both ordinary and partial differential equations. This means that highly accurate solutions to many unknown differential equations can be obtained instantaneously without retraining an entire network. We demonstrate the efficacy of the proposed deep learning approach by solving several real-world problems, such as first- and second-order linear ordinary equations, the Poisson equation, and the time-dependent Schrodinger complex-value partial differential equation.
翻译:高效、准确地解决差异方程式是科学研究许多领域进展的核心,从古典动态系统到量子力学。人们热衷于利用物理进化神经网络(PINNs)来解决这些问题,因为这些网络比传统的数字方法提供了许多好处。尽管它们对于解决差异方程式具有潜在好处,但转移学习正在探讨之中。在本研究中,我们提出了一个转让学习PINN总框架,它导致对普通和部分差异方程式的线性系统进行一线性推断。这意味着许多未知差异方程式的高度准确解决方案可以在不对整个网络进行再培训的情况下即时获得。我们通过解决一些现实世界问题,例如一等和二等等普通线性方程式、 Poisson 方程式和时间依赖的Schrodinger复杂价值部分差异方程式,来证明拟议的深层次学习方法的有效性。