Hall-type theorems for fast dynamic matching and applications

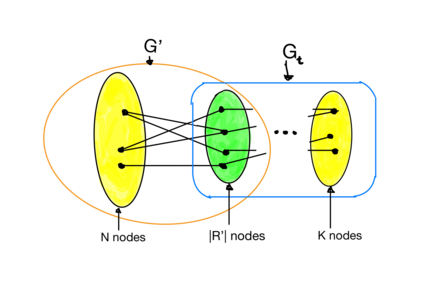
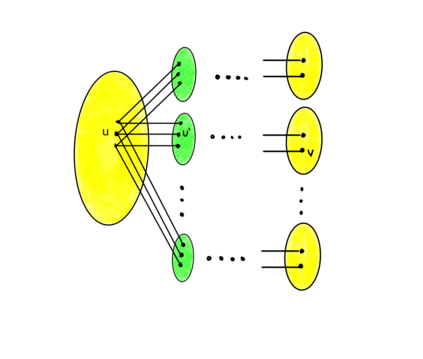
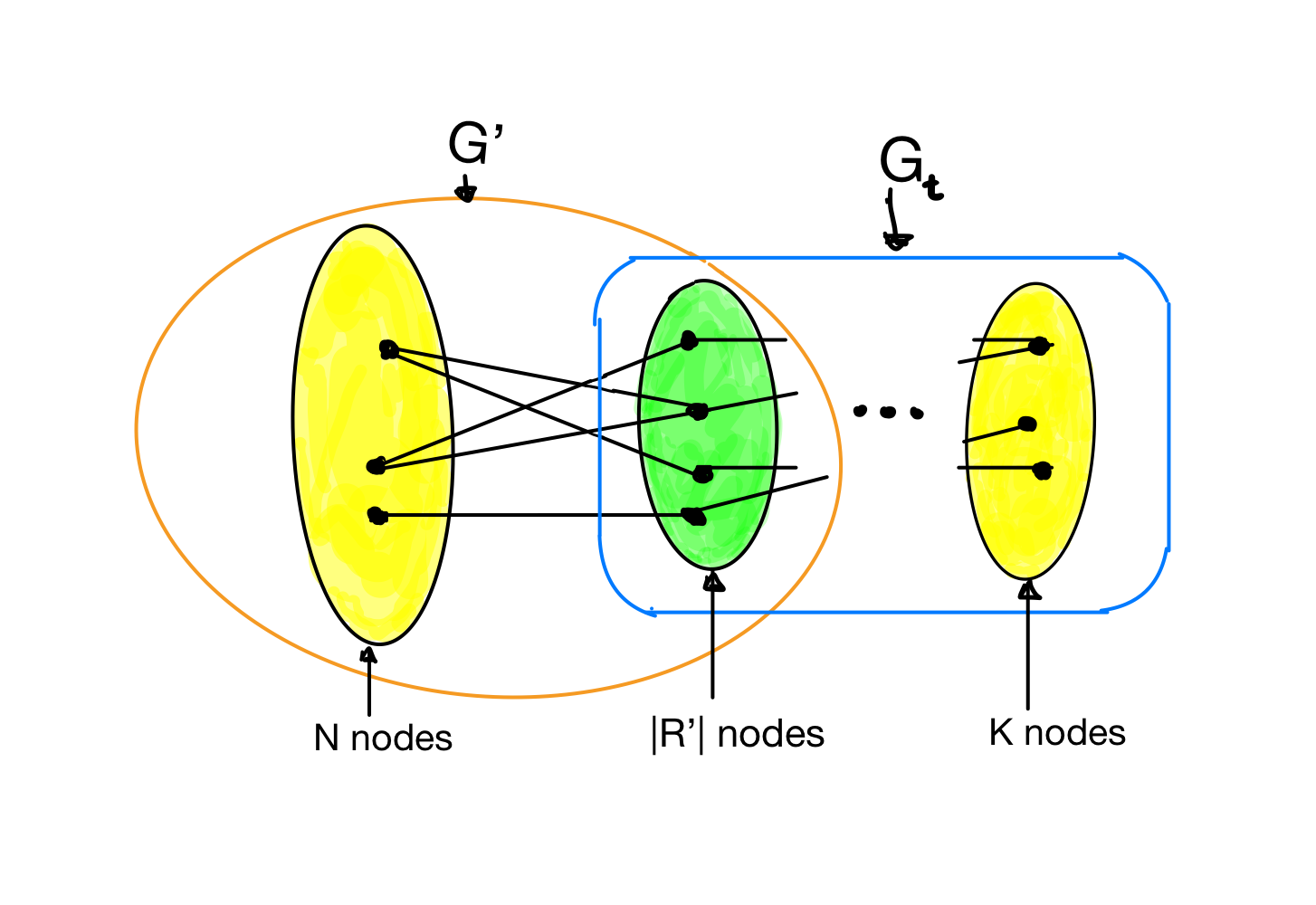
We establish relations between two properties of bipartite graphs: expansion and dynamic matching. The latter is defined as follows. In a bipartite graph $G$, left nodes represent clients and right nodes represent servers. Clients can be active or idle and they can switch between the two states. When a client becomes active a neighbor server has to be assigned to it in an online manner, and when a client becomes idle the assigned neighbor is released. $G$ has dynamic matching up to $K$ with load $r$ if assignments can always be made so that no server is ever assigned to more than $r$ clients, assuming that at most $K$ clients can be active at any given moment. A bipartite graph is a $(K, \gamma)$ expander if any subset $S$ of left nodes with size at most $K$ has at least $\gamma \cdot \# S$ neighbors. Feldman, Friedman and Pippenger (SIAM J Discrete Math., 1988] have shown that any $(K,1)$ expander has dynamic matching up to $K$ with load $3$. If we replace every right node by 3 clones, we get matching with load $1$, i.e.,\ standard matching. Unfortunately their matching algorithm is slow, running in time $\exp(K \cdot \log N)$. Our main result is that any $(2K+1, 2D/3 + 2)$ expander has dynamic matching up to $K$ with load $O(\log N)$ and a much faster matching with runtime $poly(\log N, D)$ ($N$ is the number of left nodes, and $D$ is the left degree). Even though the expansion factor and the load are larger than in [FFP88], expanders as required in our result can be constructed explicitly with good parameters for applications. Our result gives for the first time a solution to the main open problem in [FFP88]. We give two applications. The first one is in the area of non-blocking networks, and the second one is about one-probe storage schemes for dynamic sets.