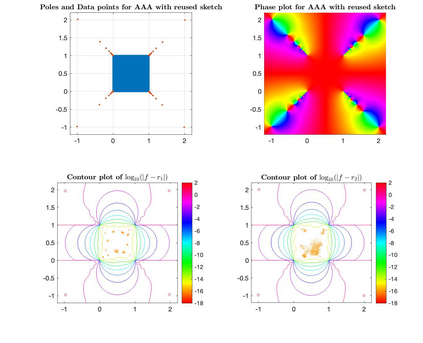
Randomized algorithms in numerical linear algebra can be fast, scalable and robust. This paper examines the effect of sketching on the right singular vectors corresponding to the smallest singular values of a tall-skinny matrix. We devise a fast algorithm for finding the trailing right singular vectors using randomization and examine the quality of the solution using multiplicative perturbation theory. For an $m\times n$ ($m\geq n$) matrix, the algorithm runs with complexity $O(mn\log n +n^3)$ which is faster than the standard $O(mn^2)$ methods. In applications, numerical experiments show great speedups including a $30\times$ speedup for the AAA algorithm and $10\times$ speedup for the total least squares problem.
翻译:数字线性代数中的随机算法可以快速、可缩放和稳健。 本文审视了绘制与高斯基尼矩阵最小单值相对应的右单向矢量图的效果。 我们设计了一个快速算法, 使用随机化来查找末端的右单向量, 并使用多复制性扰动理论来检查解决方案的质量。 对于 $m\time n$ ($m\geq n$) 矩阵来说, 该算法运行的复杂度为$O( mn\log n +n ⁇ 3) $, 高于标准的$O (m\\\ 2) 方法。 在应用中, 数字实验显示了巨大的加速, 包括 AAA 算法的30\ times $ 加速度, 和 10\ times $ ($) 快速度, 用于整个最小方块问题 。