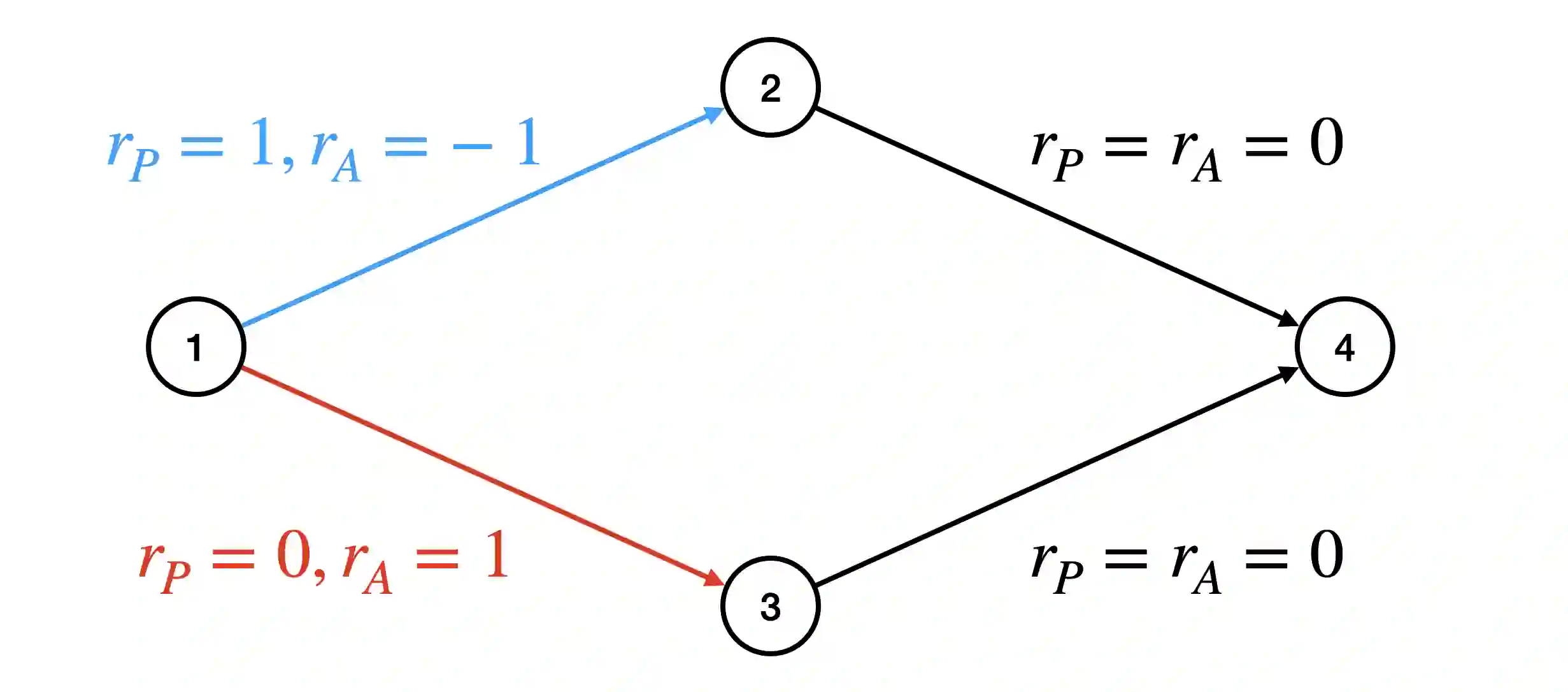
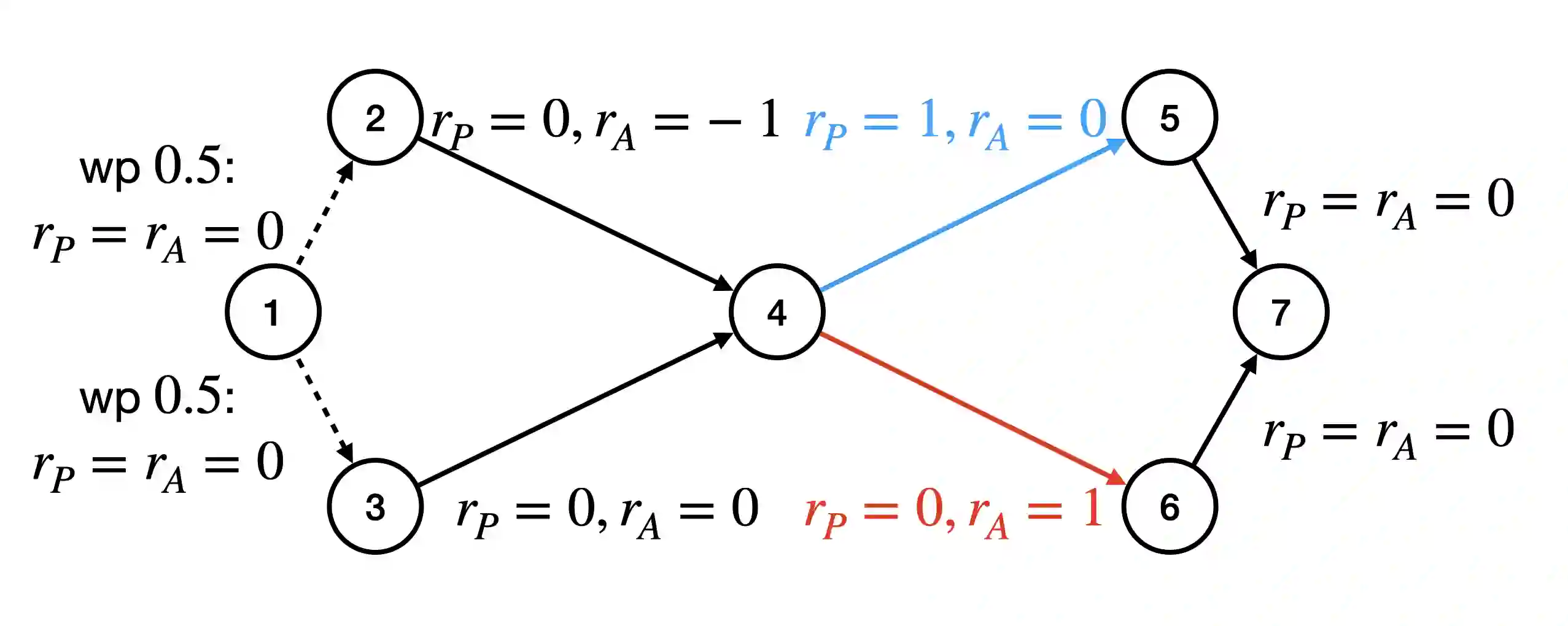
We consider the problem of planning with participation constraints introduced in [Zhang et al., 2022]. In this problem, a principal chooses actions in a Markov decision process, resulting in separate utilities for the principal and the agent. However, the agent can and will choose to end the process whenever his expected onward utility becomes negative. The principal seeks to compute and commit to a policy that maximizes her expected utility, under the constraint that the agent should always want to continue participating. We provide the first polynomial-time exact algorithm for this problem for finite-horizon settings, where previously only an additive $\varepsilon$-approximation algorithm was known. Our approach can also be extended to the (discounted) infinite-horizon case, for which we give an algorithm that runs in time polynomial in the size of the input and $\log(1/\varepsilon)$, and returns a policy that is optimal up to an additive error of $\varepsilon$.
翻译:我们考虑了在[张等人,2022] 中引入的参与限制下的规划问题。在这个问题上,一位主选择了Markov决策程序中的行动,导致本金和代理分别使用不同的公用事业。然而,代理商可以并且将选择在预期的今后效用出现负时结束这一过程。主机试图计算并承诺执行一个政策,使预期效用最大化,而该代理商始终希望继续参与的制约下。我们为有限象子设置的这个问题提供了第一个多米时间精确算法,以前只知道一个添加值$\varepsilon$-accession 算法。我们的方法也可以扩展至(折扣的)无限象子案件,为此我们给出的算法在输入大小和$\log(1/\varepsilon)$($/\ varepsilon) 之间可以运行一个时数倍的算法,并返回一个最优于美元($\varepsilon)的添加错误的政策。