Finite element approximation of a phase field model for tumour growth

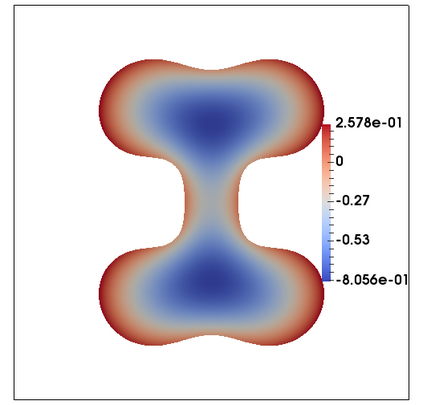
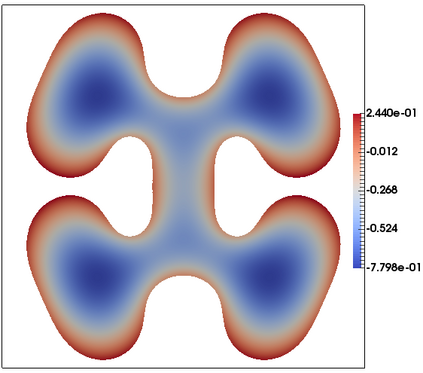
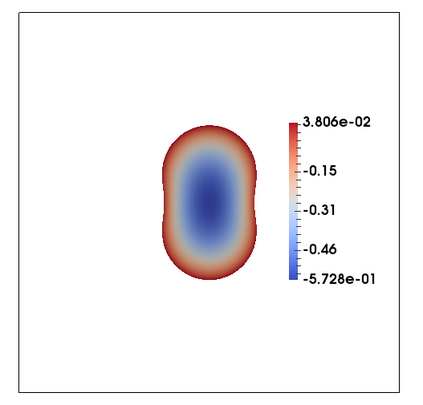
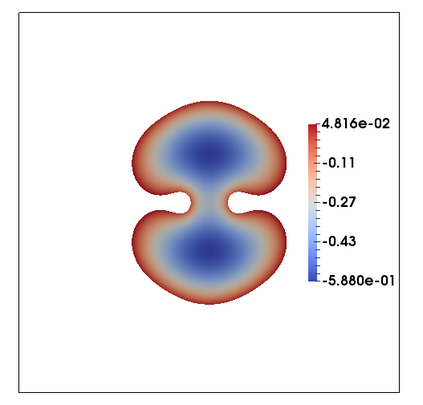
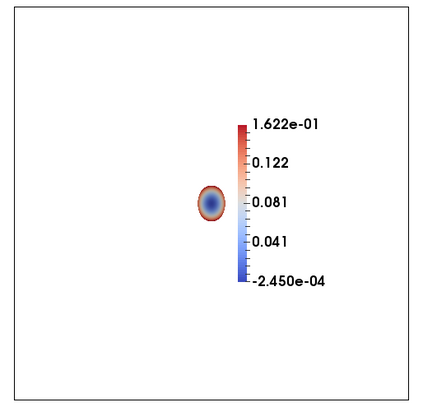
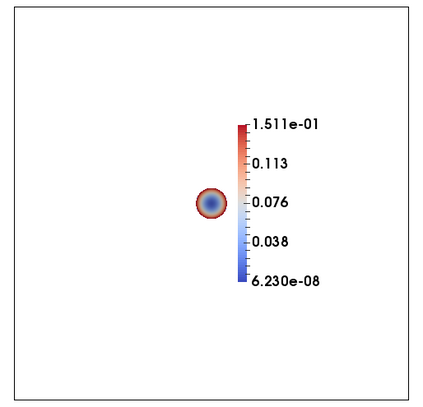
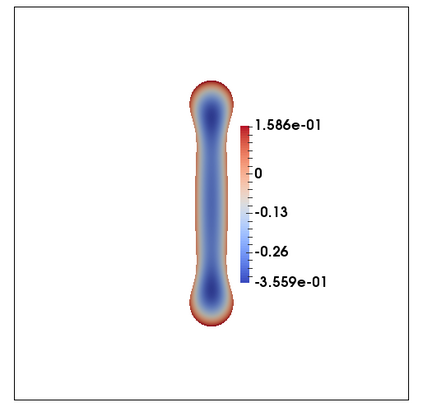
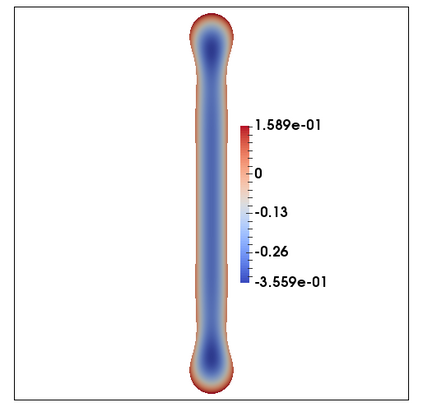
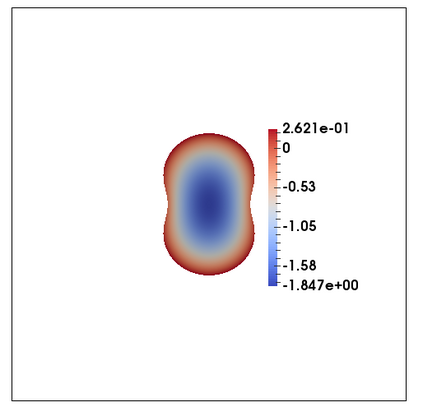
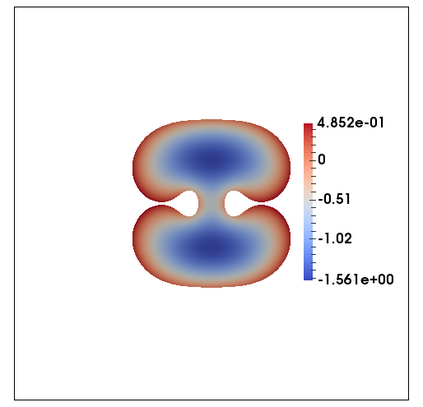
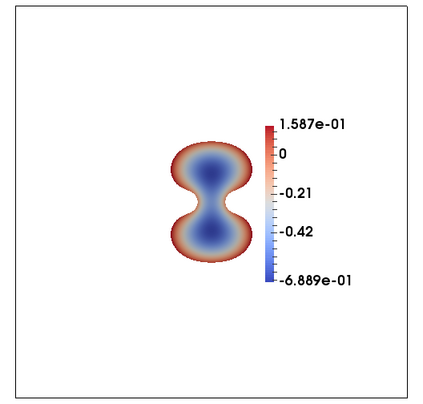
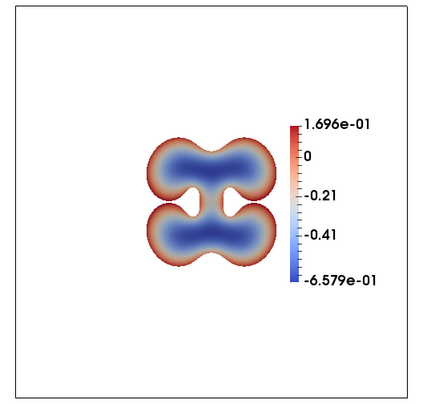
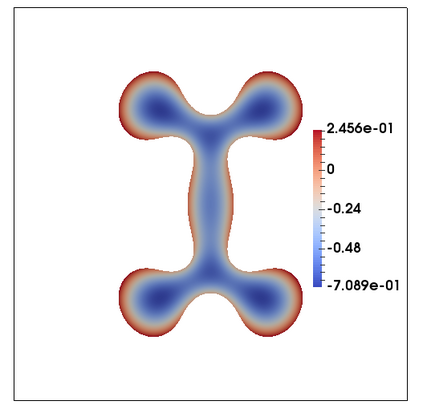
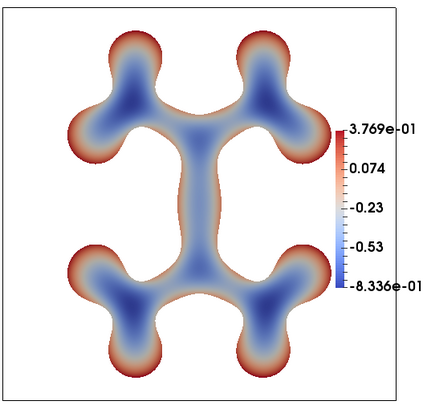
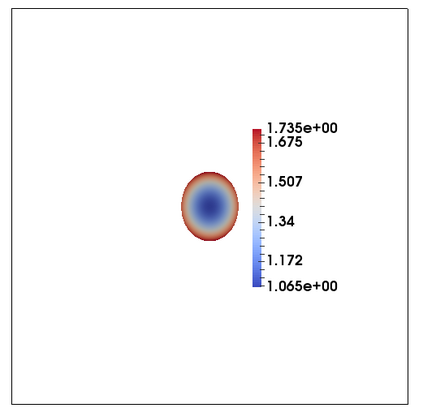
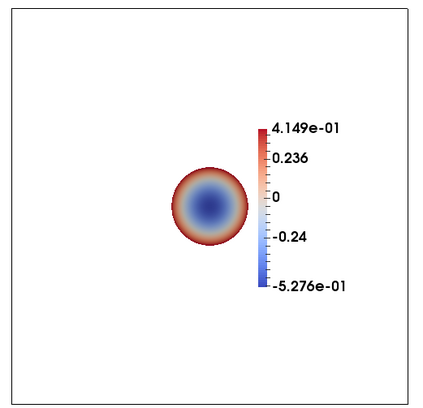
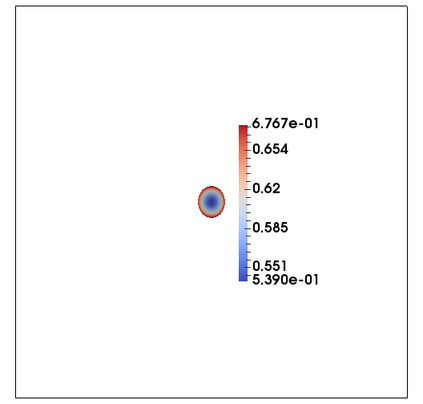
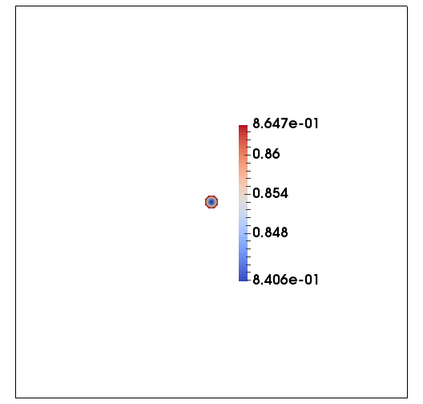
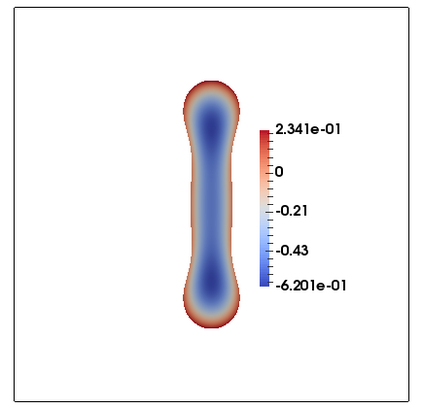
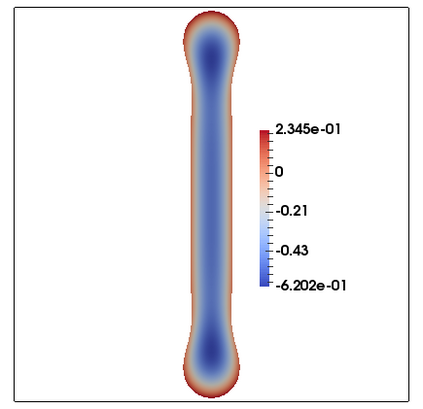
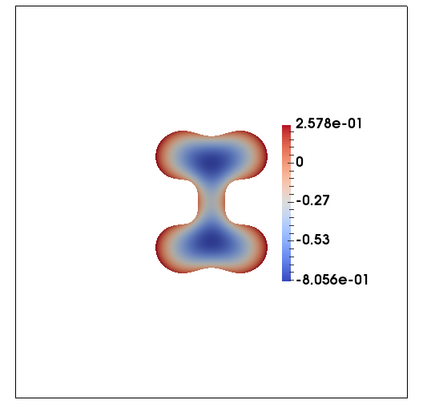
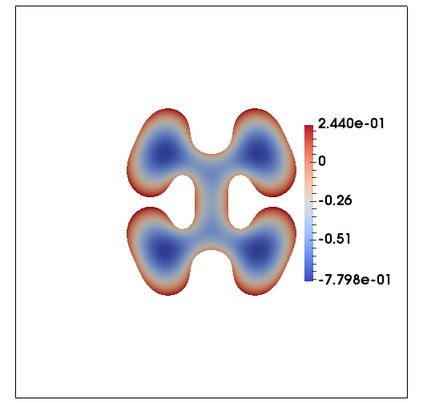
We consider a fully practical finite element approximation of a diffuse interface model for tumour growth that takes the form of a degenerate parabolic system. In addition to showing stability bounds for the approximation, we prove convergence, and hence existence of a solution to this system in two space dimensions. Several numerical experiments demonstrate the practicality and robustness of the proposed method.