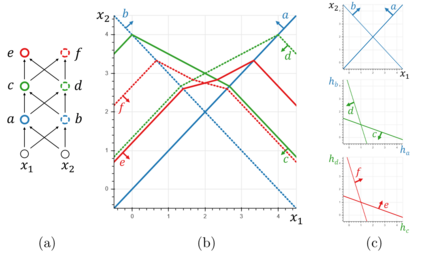
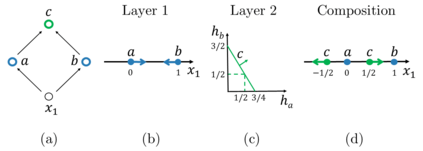
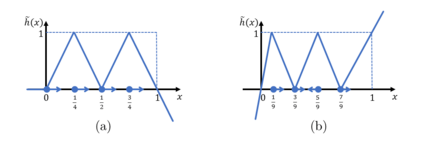
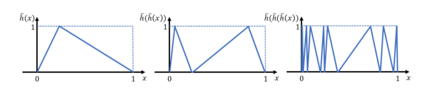
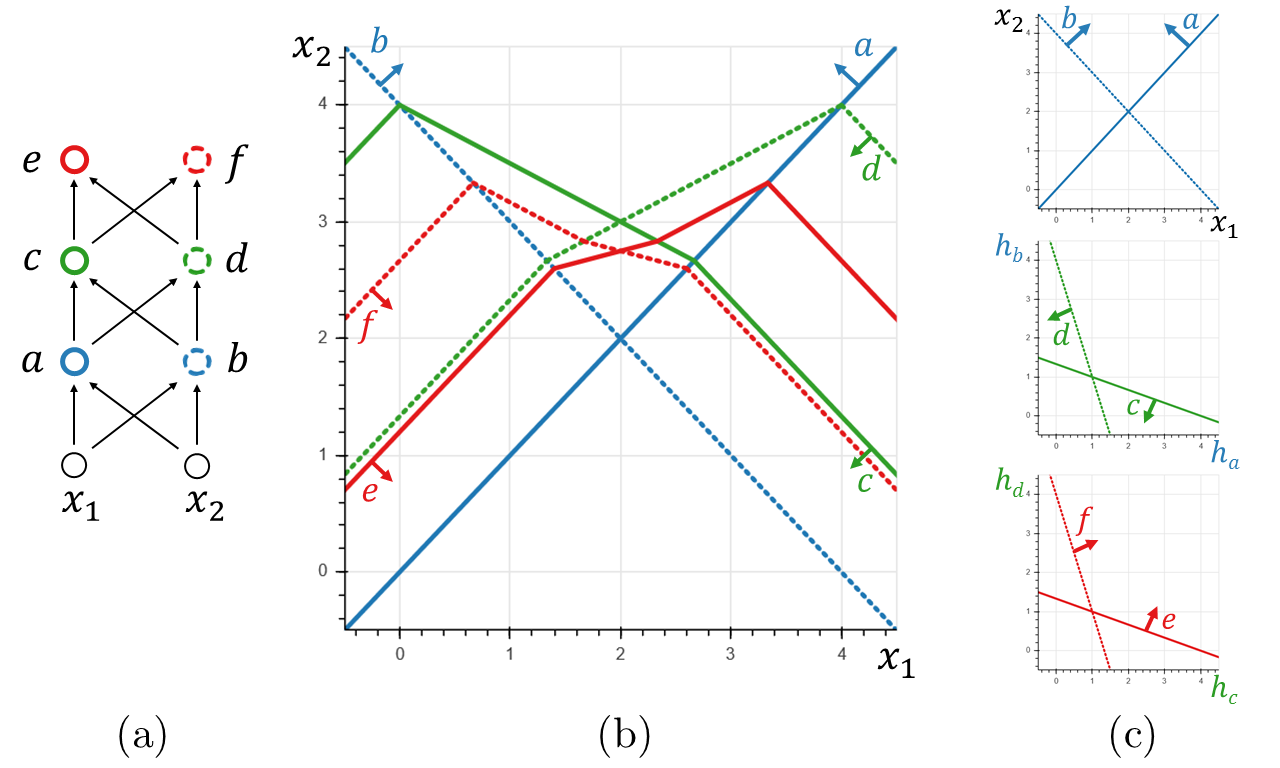
We investigate the complexity of deep neural networks (DNN) that represent piecewise linear (PWL) functions. In particular, we study the number of linear regions, i.e. pieces, that a PWL function represented by a DNN can attain, both theoretically and empirically. We present (i) tighter upper and lower bounds for the maximum number of linear regions on rectifier networks, which are exact for inputs of dimension one; (ii) a first upper bound for multi-layer maxout networks; and (iii) a first method to perform exact enumeration or counting of the number of regions by modeling the DNN with a mixed-integer linear formulation. These bounds come from leveraging the dimension of the space defining each linear region. The results also indicate that a deep rectifier network can only have more linear regions than every shallow counterpart with same number of neurons if that number exceeds the dimension of the input.
翻译:我们调查深神经网络的复杂性,这些网络代表了片断线性(PWL)功能。特别是,我们研究由DNN所代表的PWL函数在理论上和经验上都能达到的线性区域数目,即碎片。我们提出(一) 纠正网络上最大线性区域数目的上下界限,其精确度为一维投入的精确度;(二) 多层峰值网络的首个上界;以及(三) 通过以混合整数线性配方模拟DNN,对区域数目进行精确的查点或计数的第一个方法。这些界限来自利用确定每一线性区域的空间的尺寸。结果还表明,深整数网络的线性区域只能比每个具有相同神经元的浅色对应方的线性区域更多,如果这个数字超过输入的维度。