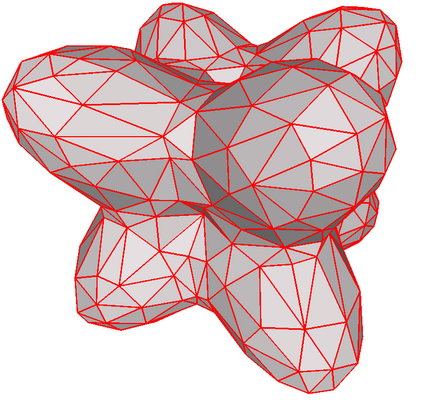
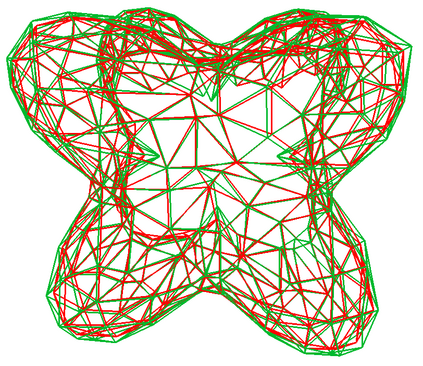
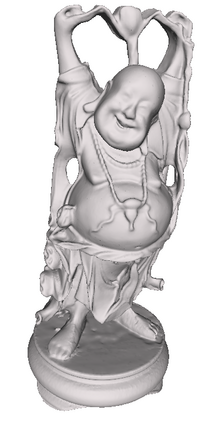
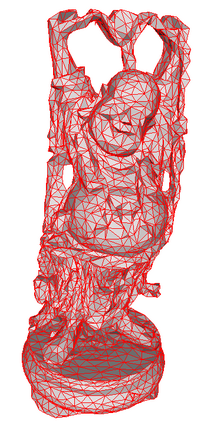
In this paper, we propose a stochastic geometric iterative method to approximate the high-resolution 3D models by finite Loop subdivision surfaces. Given an input mesh as the fitting target, the initial control mesh is generated using the mesh simplification algorithm. Then, our method adjusts the control mesh iteratively to make its finite Loop subdivision surface approximates the input mesh. In each geometric iteration, we randomly select part of points on the subdivision surface to calculate the difference vectors and distribute the vectors to the control points. Finally, the control points are updated by adding the weighted average of these difference vectors. We prove the convergence of our method and verify it by demonstrating error curves in the experiment. In addition, compared with an existing geometric iterative method, our method has a faster fitting speed and higher fitting precision.
翻译:在本文中, 我们提出一种随机的几何迭接法, 以定点环形子分割表面来近似高分辨率 3D 模型。 以输入网格作为适配目标, 初始控制网格是使用网格简化算法生成的。 然后, 我们的方法对控制网格进行迭接调整, 使其有限的环形子分割面接近输入网格。 在每次几何迭代法中, 我们随机地选择了分区表面的部分点, 以计算差分矢量, 并将矢量分配到控制点 。 最后, 控制点通过添加这些差分矢量的加权平均值来更新 。 我们证明我们方法的趋同, 并通过实验中显示错误曲线来验证它。 此外, 与现有的几何迭接法相比, 我们的方法速度更快, 且精确度更高 。