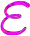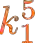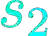We consider the watchman route problem for a $k$-transmitter watchman: standing at point $p$ in a polygon $P$, the watchman can see $q\in P$ if $\overline{pq}$ intersects $P$'s boundary at most $k$ times -- $q$ is $k$-visible to $p$. Traveling along the $k$-transmitter watchman route, either all points in $P$ or a discrete set of points $S\subset P$ must be $k$-visible to the watchman. We aim for minimizing the length of the $k$-transmitter watchman route. We show that even in simple polygons the shortest $k$-transmitter watchman route problem for a discrete set of points $S\subset P$ is NP-complete and cannot be approximated to within a logarithmic factor (unless P=NP), both with and without a given starting point. Moreover, we present a polylogarithmic approximation for the $k$-transmitter watchman route problem for a given starting point and $S\subset P$ with approximation ratio $O(\log^2(|S|\cdot n) \log\log (|S|\cdot n) \log(|S|+1))$ (with $|P|=n$).
翻译:我们考虑对一个 $k$ Transmisser 监视器的监视器路线问题: 在一个多边方美元中站在点上 $ p$, 观察器员可以看到$ p$ 如果$\ overline{pq} 美元以美元乘以美元乘以美元乘以美元 -- 美元是K美元看得上美元。 在一个 $- Transmisser 监视器的路线上旅行, 要么是所有点以美元计价, 要么是一组离散的点数 $S\ submisser P$ (S\ subset P=NP=NP) 。 此外, 我们提出一个美元以美元计价和 美元以美元计价的多方位近路长。 我们显示,即使在简单的多边方美元中, 一个离散点的 $S\ subsetc=_\\\\\ 美元观察器的路线问题, 也是Nk- trainxrickrickr=_\\ 美元。