Practical KMP/BM Style Pattern-Matching on Indeterminate Strings

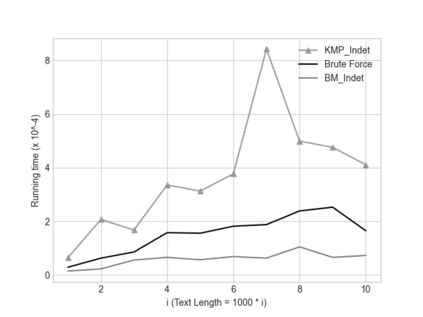
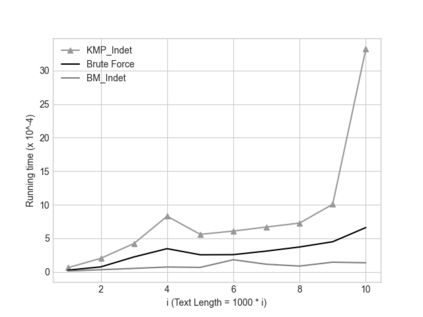
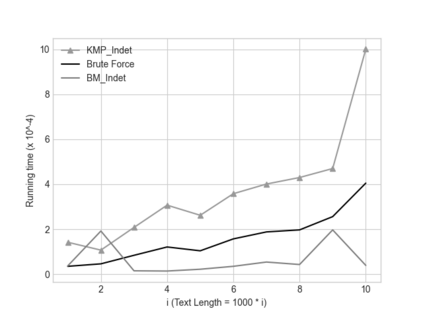
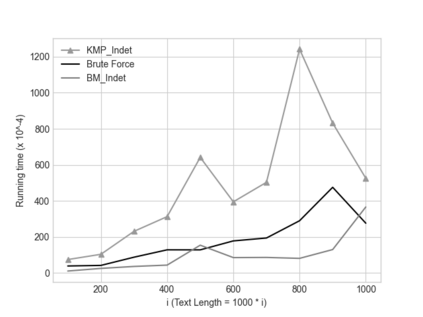
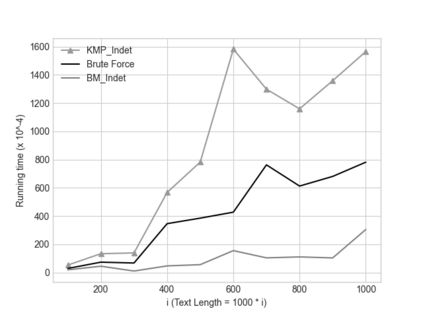
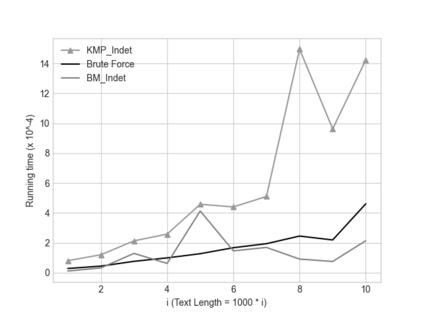
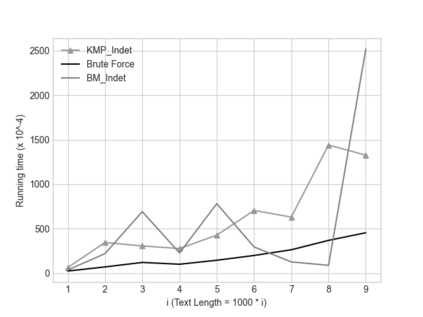
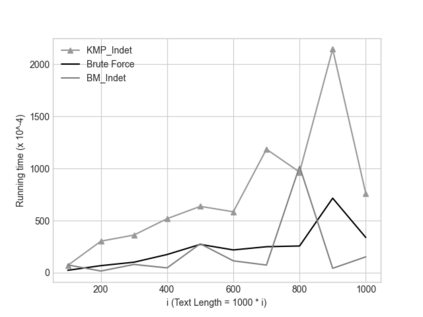
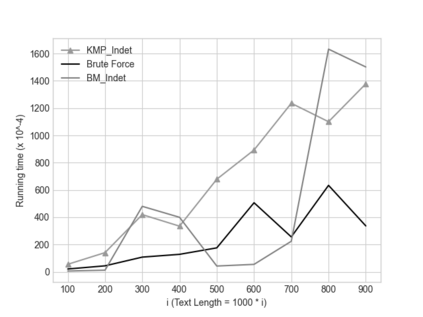
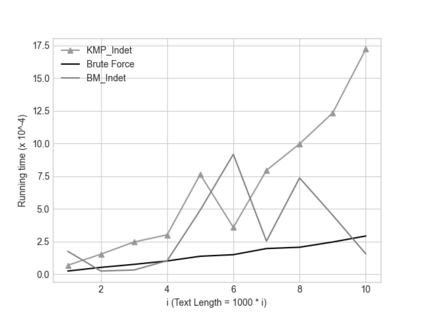
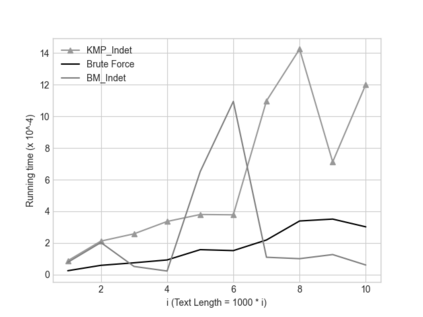
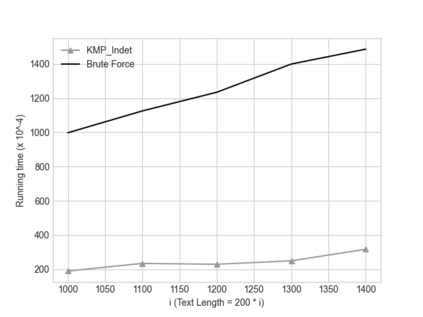
In this paper we describe two simple, fast, space-efficient algorithms for finding all matches of an indeterminate pattern $\s{p} = \s{p}[1..m]$ in an indeterminate string $\s{x} = \s{x}[1..n]$, where both \s{p} and \s{x} are defined on a "small" ordered alphabet $\Sigma$ -- say, $\sigma = |\Sigma| \le 9$. Both algorithms depend on a preprocessing phase that replaces $\Sigma$ by an integer alphabet $\Sigma_I$ of size $\sigma_I = \sigma$ which (reversibly, in time linear in string length) maps both \s{x} and \s{p} into equivalent regular strings \s{y} and \s{q}, respectively, on $\Sigma_I$, whose maximum (indeterminate) letter can be expressed in a 32-bit word (for $\sigma \le 4$, thus for DNA sequences, an 8-bit representation suffices). We first describe an efficient version \textsc{KMP\_Indet} of the venerable Knuth-Morris-Pratt algorithm to find all occurrences of \s{q} in \s{y} (that is, of \s{p} in \s{x}), but, whenever necessary, using the prefix array, rather than the border array, to control shifts of the transformed pattern \s{q} along the transformed string \s{y}. %Although requiring $\O(m^2n)$ time in the theoretical worst case, in cases of practical interest \textsc{KMP\_Indet} executes in $\O(n)$ time. We go on to describe a similar efficient version \textsc{BM\_Indet} of the Boyer-Moore algorithm that turns out to execute significantly faster than \textsc{KMP\_Indet} over a wide range of test cases. %A noteworthy feature is that both algorithms require very little additional space: $\Theta(m)$ words. We conjecture that a similar approach may yield practical and efficient indeterminate equivalents to other well-known pattern-matching algorithms, in particular the several variants of Boyer-Moore.