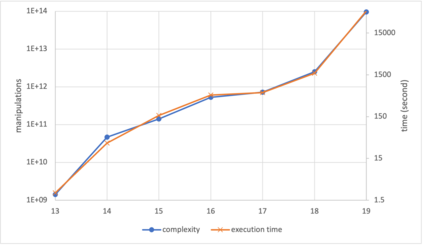
Solving a system of $m$ multivariate quadratic equations in $n$ variables (the $\mathcal MQ$ problem) is one of the main challenges of algebraic cryptanalysis. The XL algorithm (XL for short) is a major approach for solving the $\mathcal MQ$ problem with linearization over a coefficient field. Furthermore, the hybrid approach with XL (h-XL) is a variant of XL guessing some variables beforehand. In this paper, we present a variant of h-XL, which we call the polynomial XL (PXL). In PXL, the whole $n$ variables are divided into $k$ variables to be fixed and the remaining $n-k$ variables as "main variables", and we generate the Macaulay matrix with respect to the $n-k$ main variables over a polynomial ring of the $k$ variables. By eliminating some columns of the Macaulay matrix over the polynomial ring before guessing $k$ variables, the amount of manipulations required for each guessed value can be reduced. Our complexity analysis indicates that PXL is efficient on the system with $n \approx m$. For example, on systems over ${\mathbb F}_{2^8}$ with $n=m=80$, the number of manipulations required by the hybrid approaches with XL and Wiedemann XL and PXL is estimated as $2^{252}$, $2^{234}$, and $2^{220}$, respectively.
翻译:解决一个以美元变量( $\ mathcal MQ$ 问题) 中多变二次方程的系统, 以美元变量( $\ mathcal MQ$ 问题) 解决问题。 XL 算法( XL 简称) 是解决 $ mathcal MQ$ 在系数字段线性化问题的主要方法 。 此外, 与 XL (h- XL) 混合法( XL) 是一个变量的变方, 预测某些变量 。 在本文中, 我们提出了一个 h- XL 变量的变方, 我们称之为 多元 XL (美元) (美元) 。 在计算 $xL (美元) (美元) 之前, 我们将整个 美元变量分为 $k美元变量, 其余的 n- k美元变量作为“ 主要变量 ” 。 我们生成了澳门矩阵矩阵, 美元主要变量在 $kn- kn 变量圈 。 通过在 pool20 环 之前在 yn $ $ $x} ( Pxx} 中消除澳门矩阵 矩阵中的某些列 矩阵, 每个猜测值需要的操作量 $ $ $ $ 2xxxxx 。