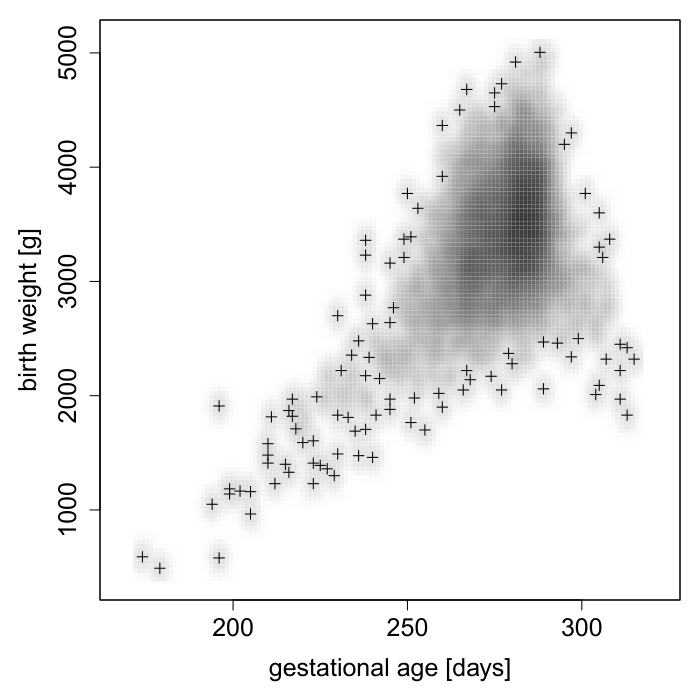
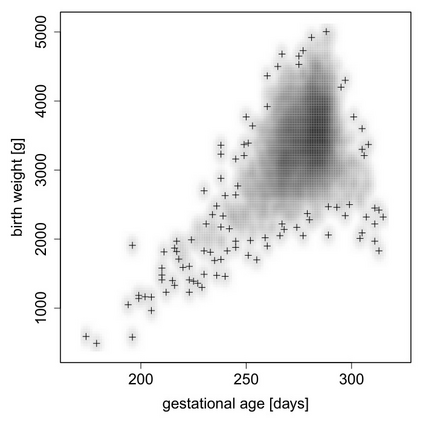
In this article, we analyze perinatal data with birth weight (BW) as primarily interesting response variable. Gestational age (GA) is usually an important covariate and included in polynomial form. However, in opposition to this univariate regression, bivariate modeling of BW and GA is recommended to distinguish effects on each, on both, and between them. Rather than a parametric bivariate distribution, we apply conditional copula regression, where marginal distributions of BW and GA (not necessarily of the same form) can be estimated independently, and where the dependence structure is modeled conditional on the covariates separately from these marginals. In the resulting distributional regression models, all parameters of the two marginals and the copula parameter are observation-specific. Besides biometric and obstetric information, data on drinking water contamination and maternal smoking are included as environmental covariates. While the Gaussian distribution is suitable for BW, the skewed GA data are better modeled by the three-parametric Dagum distribution. The Clayton copula performs better than the Gumbel and the symmetric Gaussian copula, indicating lower tail dependence (stronger dependence when both variables are low), although this non-linear dependence between BW and GA is surprisingly weak and only influenced by Cesarean section. A non-linear trend of BW on GA is detected by a classical univariate model that is polynomial with respect to the effect of GA. Linear effects on BW mean are similar in both models, while our distributional copula regression also reveals covariates' effects on all other parameters.
翻译:在本篇文章中,我们分析出生体重(BW)的围产期数据,将其作为主要有趣的反应变量。 妊娠年龄( GA) 通常是一个重要的共变变量, 并且以多式形式包含。 但是, 与这种单向回归相反, BW 和 GA 的双变模型被建议区分对两者以及两者的影响。 我们采用有条件的双差双差分布, 即可以独立地估算BW 和 GA的边际分布( 不一定相同形式), 依赖性结构以与这些边际分开的共变形为模型。 在由此形成的分布回归模型中, 两个边际参数和 Cocula参数的所有参数都是特定观测的。 除了生物和产科信息之外, 饮用水污染和孕产妇吸烟的数据也作为环境变异。 虽然高差分布适合BWW, 斜度的GA数据的边际分布由三种对等值分布, 但Cylton Coula 的线比 和 symyalal 直径的直径影响要好得多, 但是, 直径直径直径直系的直径直径直系的直径直系的直径直系( 直系直系直系的直系的直系的直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系直系) 。