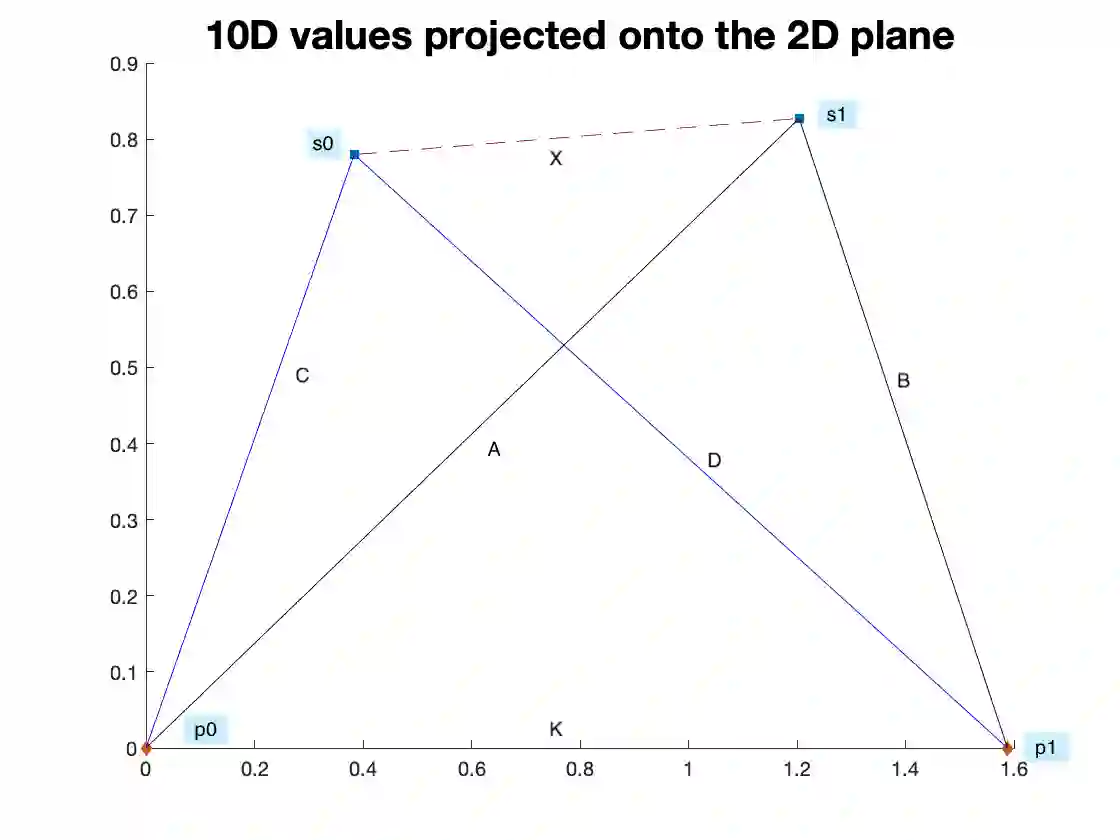
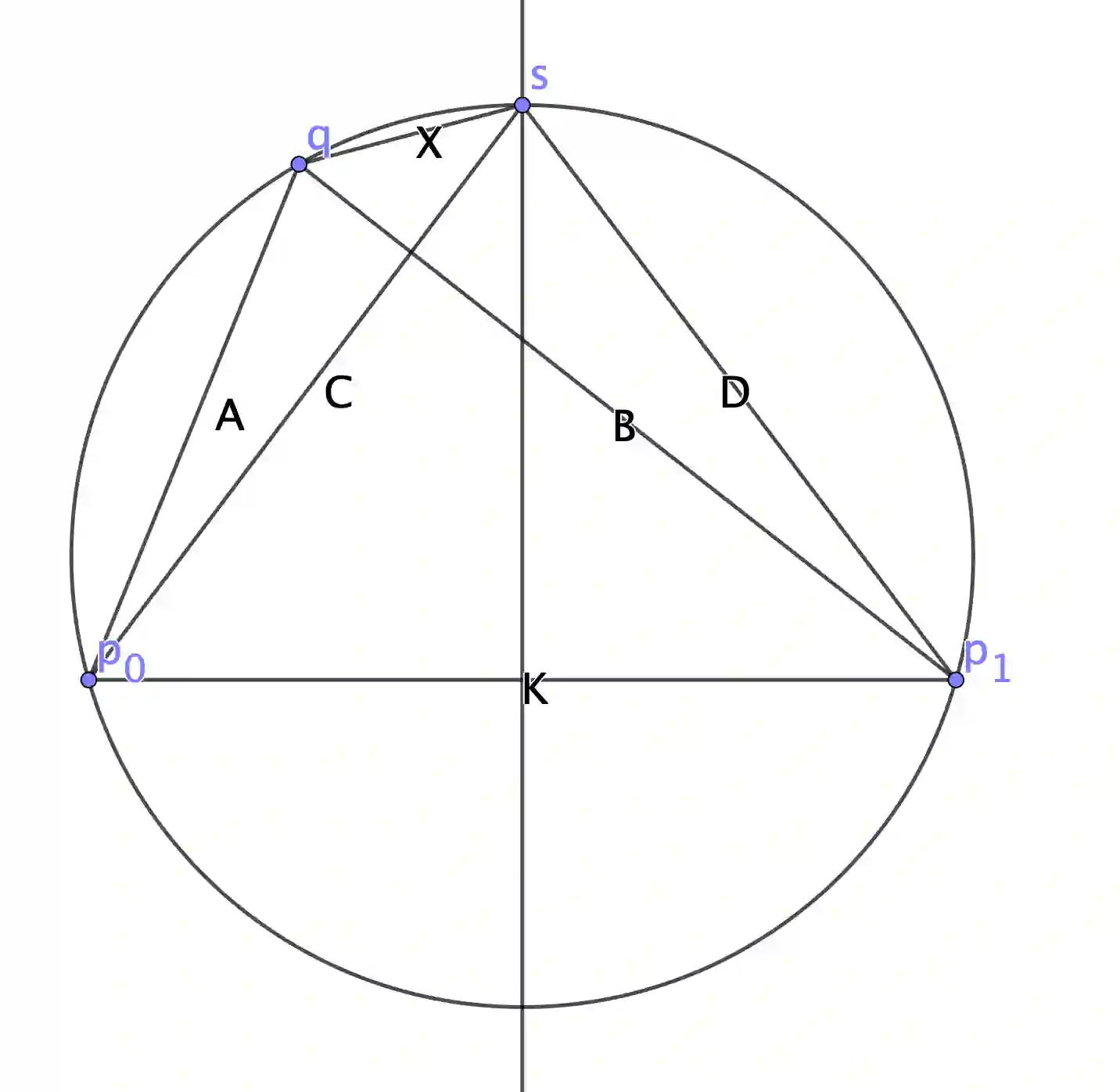
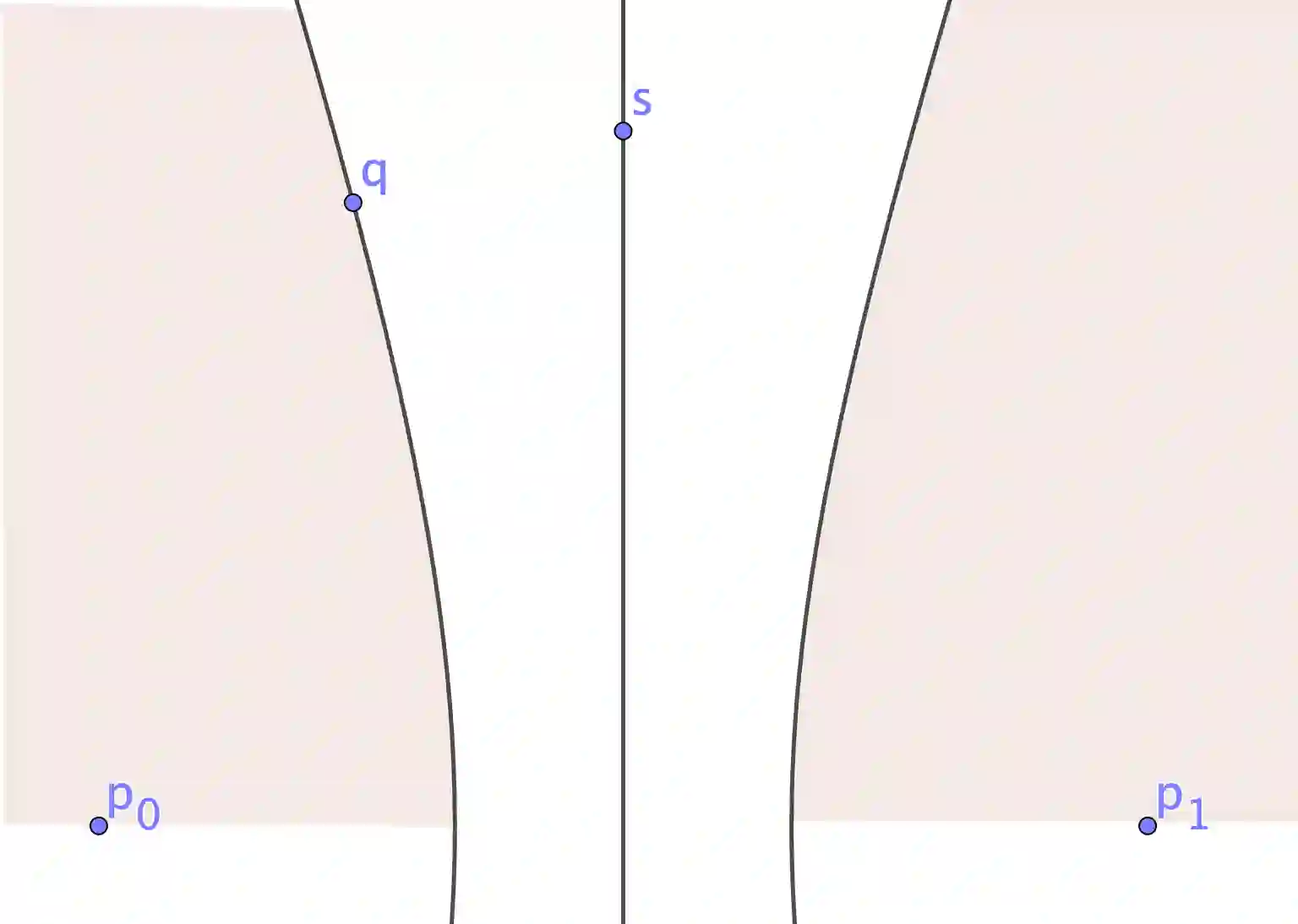
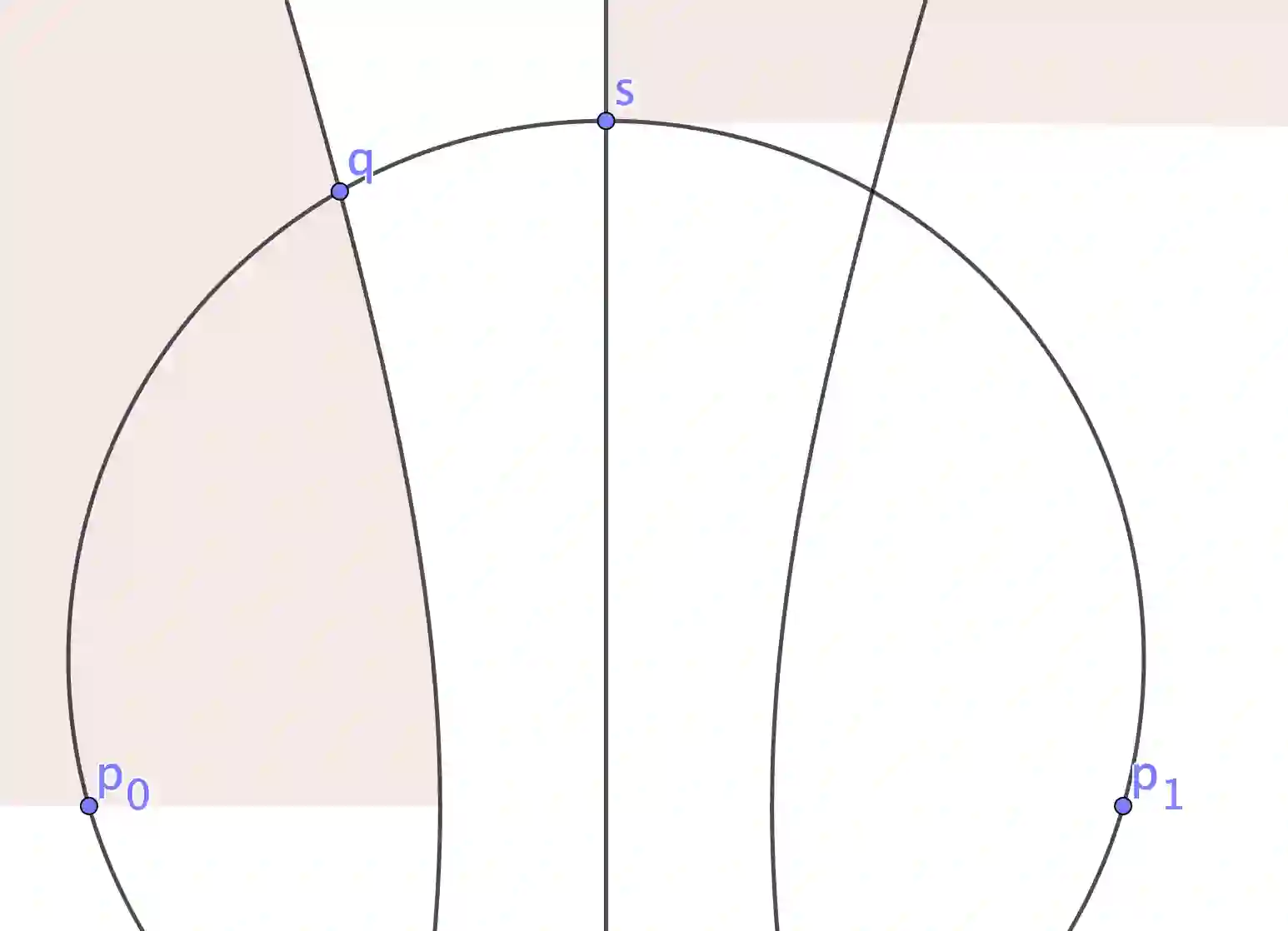
For many years, exact metric search relied upon the property of triangle inequality to give a lower bound on uncalculated distances. Two exclusion mechanisms derive from this property, generally known as pivot exclusion and hyperplane exclusion. These mechanisms work in any proper metric space and are the basis of many metric indexing mechanisms. More recently, the Ptolemaic and four-point lower bound properties have been shown to give tighter bounds in some subclasses of metric space. Both triangle inequality and the four-point lower bound directly imply straightforward partitioning mechanisms: that is, a method of dividing a finite space according to a fixed partition, in order that one or more classes of the partition can be eliminated from a search at query time. However, up to now, no partitioning principle has been identified for the Ptolemaic inequality, which has been used only as a filtering mechanism. Here, a novel partitioning mechanism for the Ptolemaic lower bound is presented. It is always better than either pivot or hyperplane partitioning. While the exclusion condition itself is weaker than Hilbert (four-point) exclusion, its calculation is cheaper. Furthermore, it can be combined with Hilbert exclusion to give a new maximum for exclusion power with respect to the number of distances measured per query.
翻译:多年来,精确的计量搜索依赖于三角不平等的属性,从而在未计算到的距离上得到较低的约束。两种排斥机制源自于这种属性,一般称为偏角排斥和超高飞机排斥。这些机制在任何适当的衡量空间中发挥作用,是许多衡量指数机制的基础。最近,多球和四点较低的约束属性显示在一些计量空间的子类中提供了更紧的界限。三角不平等和四点下界都直接意味着直截了当的分割机制:即按照固定分区划分有限空间的方法,以便从查询时间的搜索中消除一类或多类分割空间。然而,到目前为止,还没有为Potolemaic不平等确定分界线原则,而后者仅被用作过滤机制。这里介绍了Ptolemaic较低界限的新式的分隔机制。它总是比偏角或超平流分隔机制都更直接意味着直接的分割机制:即按照固定分区划分有限空间的方法,以便从查询的时间中消除一个或多个分界线。然而,迄今为止,对于Ptolemaic的不平等没有确定分界线原则,而只是作为过滤机制使用。此外,它计算出一种最廉价的距离,它可以把排斥与新的分数与新的分数结合起来,测量。