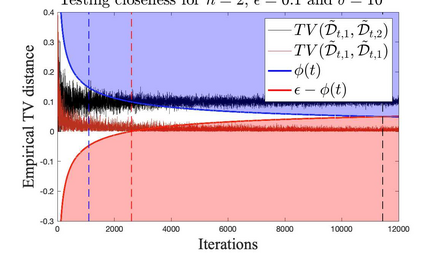
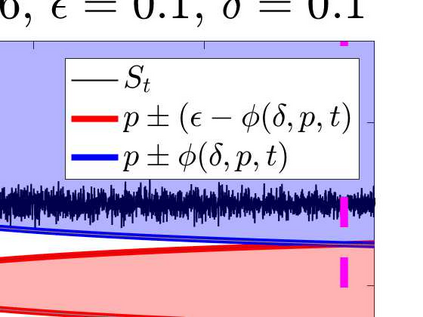
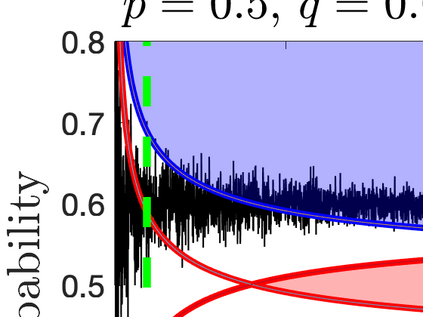
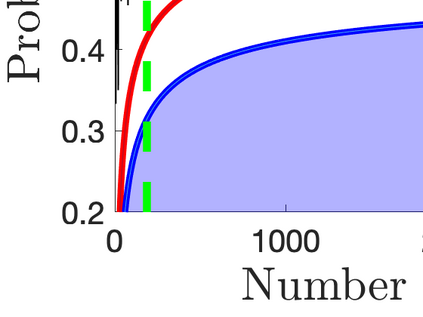
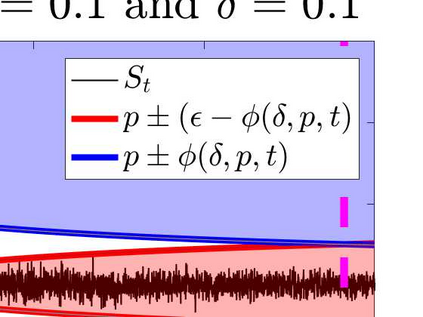
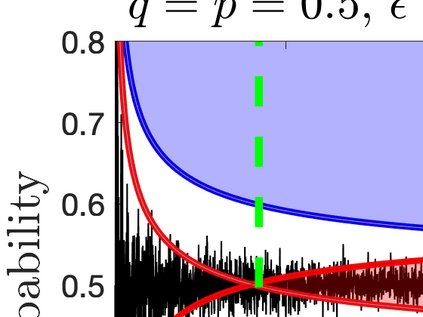
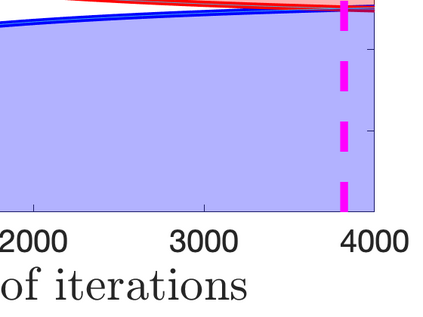
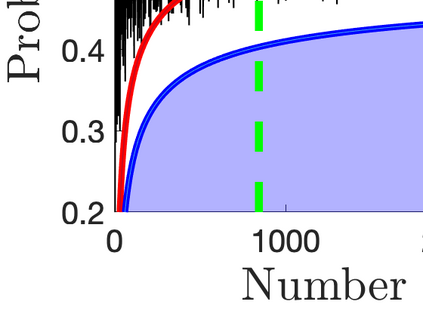
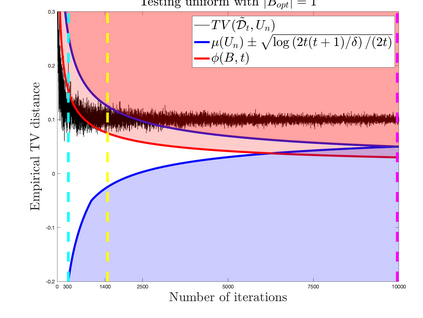
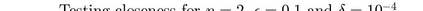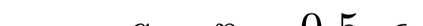What advantage do \emph{sequential} procedures provide over batch algorithms for testing properties of unknown distributions? Focusing on the problem of testing whether two distributions $\mathcal{D}_1$ and $\mathcal{D}_2$ on $\{1,\dots, n\}$ are equal or $\epsilon$-far, we give several answers to this question. We show that for a small alphabet size $n$, there is a sequential algorithm that outperforms any batch algorithm by a factor of at least $4$ in terms sample complexity. For a general alphabet size $n$, we give a sequential algorithm that uses no more samples than its batch counterpart, and possibly fewer if the actual distance $TV(\mathcal{D}_1, \mathcal{D}_2)$ between $\mathcal{D}_1$ and $\mathcal{D}_2$ is larger than $\epsilon$. As a corollary, letting $\epsilon$ go to $0$, we obtain a sequential algorithm for testing closeness when no a priori bound on $TV(\mathcal{D}_1, \mathcal{D}_2)$ is given that has a sample complexity $\tilde{\mathcal{O}}(\frac{n^{2/3}}{TV(\mathcal{D}_1, \mathcal{D}_2)^{4/3}})$: this improves over the $\tilde{\mathcal{O}}(\frac{n/\log n}{TV(\mathcal{D}_1, \mathcal{D}_2)^{2} })$ tester of \cite{daskalakis2017optimal} and is optimal up to multiplicative constants. We also establish limitations of sequential algorithms for the problem of testing identity and closeness: they can improve the worst case number of samples by at most a constant factor.
翻译:===================================================================================================================================================d================================================================================================================================l========================================================================================================================================================================================================================================