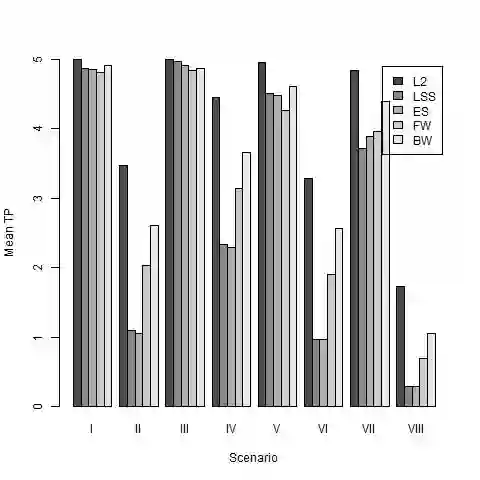
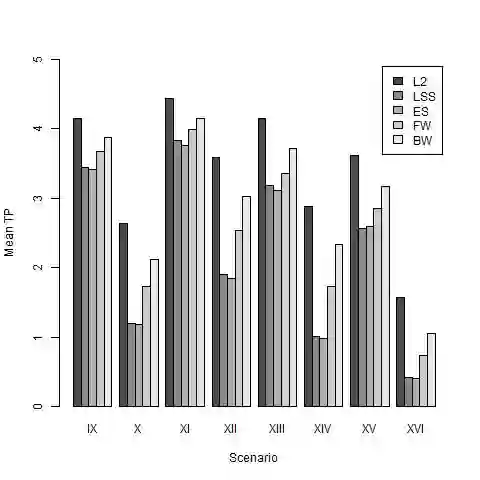
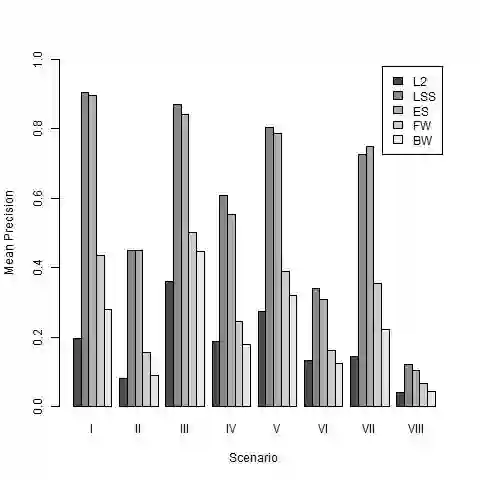
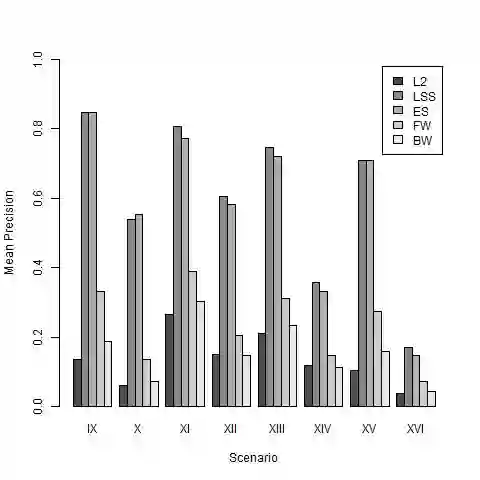
In modern data analysis, sparse model selection becomes inevitable once the number of predictors variables is very high. It is well-known that model selection procedures like the Lasso or Boosting tend to overfit on real data. The celebrated Stability Selection overcomes these weaknesses by aggregating models, based on subsamples of the training data, followed by choosing a stable predictor set which is usually much sparser than the predictor sets from the raw models. The standard Stability Selection is based on a global criterion, namely the per-family error rate, while additionally requiring expert knowledge to suitably configure the hyperparameters. Since model selection depends on the loss function, i.e., predictor sets selected w.r.t. some particular loss function differ from those selected w.r.t. some other loss function, we propose a Stability Selection variant which respects the chosen loss function via an additional validation step based on out-of-sample validation data, optionally enhanced with an exhaustive search strategy. Our Stability Selection variants are widely applicable and user-friendly. Moreover, our Stability Selection variants can avoid the issue of severe underfitting which affects the original Stability Selection for noisy high-dimensional data, so our priority is not to avoid false positives at all costs but to result in a sparse stable model with which one can make predictions. Experiments where we consider both regression and binary classification and where we use Boosting as model selection algorithm reveal a significant precision improvement compared to raw Boosting models while not suffering from any of the mentioned issues of the original Stability Selection.
翻译:在现代数据分析中,一旦预测值变量的数量非常高,稀有的模型选择就会变得不可避免。众所周知,拉索或拉普斯(Lasso)等模型选择程序往往会过度使用真实数据。值得庆祝的稳定选择会通过根据培训数据子样集汇总模型克服这些弱点,然后选择一个稳定预测数组,通常比原始模型的预测数组少得多。标准稳定选择是基于一个全球标准,即每个家庭误差率,同时额外要求专家知识来适当配置超参数。由于模型选择取决于损失函数,即预测或设置选定的 w.r.t. 某些特定损失函数不同于选定的 w.r.t. 其他一些损失函数,我们提议了一个稳定选择数变量的变式,通过一个额外的验证步骤来尊重选定的损失函数,该选项通常比原始的验证数据要少得多,该选项以详尽的搜索战略加强。我们的稳定选择值变量广泛适用,但方便用户使用。此外,我们的稳定选择变式的变式可以避免一个严重的问题,因为这样的问题会影响我们最初的稳定性选择率的精确性,在高维度的模型中,而我们则会考虑一个选择一个稳定的预估的精确的排序,我们可以避免一个比一个我们的任何结果。