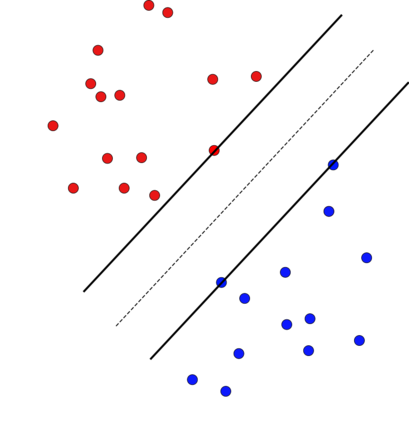
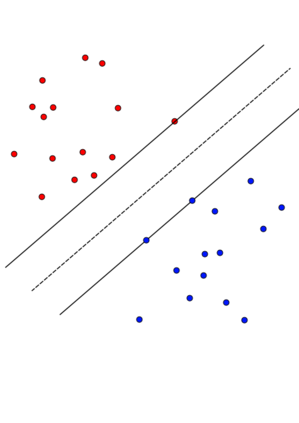
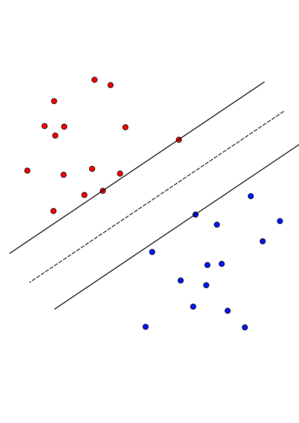
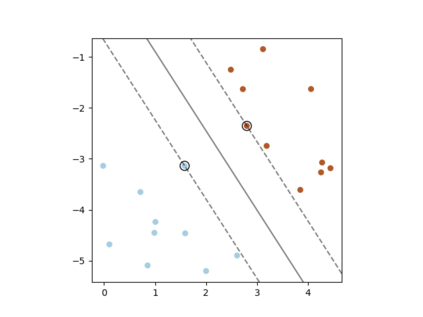
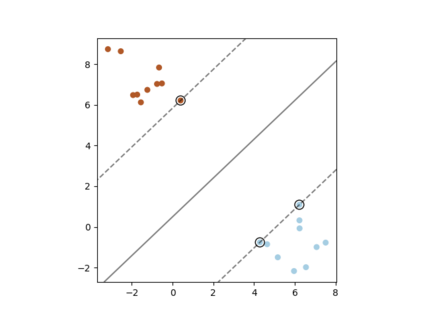
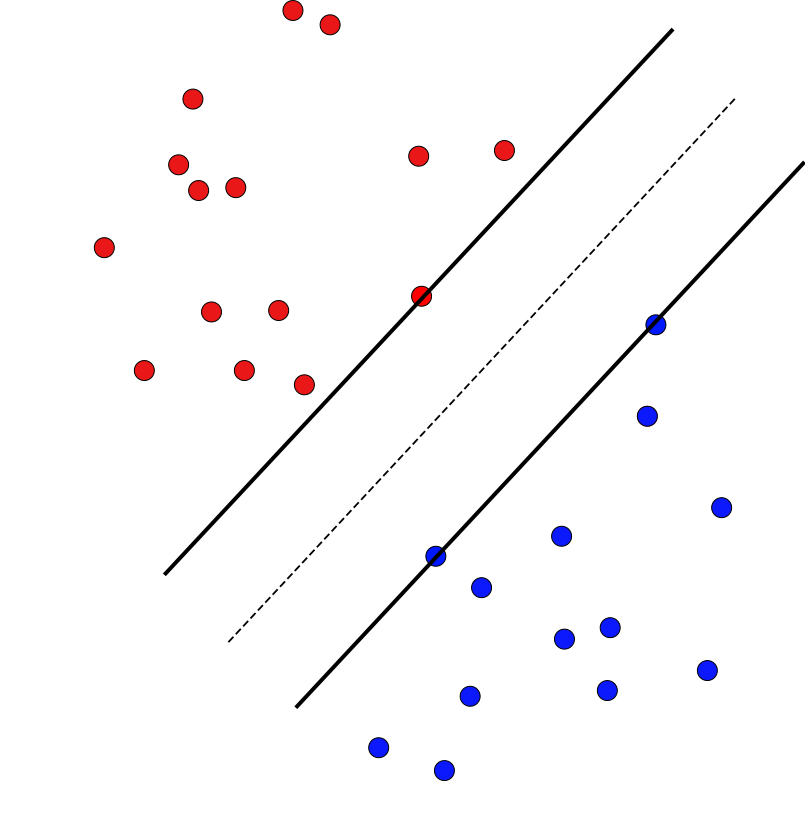
A support vector machine (SVM) is an algorithm that finds a hyperplane which optimally separates labeled data points in $\mathbb{R}^n$ into positive and negative classes. The data points on the margin of this separating hyperplane are called support vectors. We connect the possible configurations of support vectors to Radon's theorem, which provides guarantees for when a set of points can be divided into two classes (positive and negative) whose convex hulls intersect. If the convex hulls of the positive and negative support vectors are projected onto a separating hyperplane, then the projections intersect if and only if the hyperplane is optimal. Further, with a particular type of general position, we show that (a) the projected convex hulls of the support vectors intersect in exactly one point, (b) the support vectors are stable under perturbation, (c) there are at most $n+1$ support vectors, and (d) every number of support vectors from 2 up to $n+1$ is possible. Finally, we perform computer simulations studying the expected number of support vectors, and their configurations, for randomly generated data. We observe that as the distance between classes of points increases for this type of randomly generated data, configurations with fewer support vectors become more likely.
翻译:支持矢量机( SVM) 是一种算法, 它可以找到一种超大平面, 最佳地将正和负支持矢量的标签数据点分隔为$\mathb{R ⁇ n$, 以正和负类。 此分离的超高平面边边距上的数据点被称为支持矢量。 我们将支持矢量的可能配置连接到Radon 的定律上, 该定律为当一组点可以分为两类( 阳和负) 时提供保障。 如果正和负支持矢量的结壳被投射到一个分离的超平面上, 那么预测只有在超平面是最佳的时才相互交叉。 此外, 在特定的一般位置上, 我们显示 (a) 支持矢量的预测矩形柱体在精确的一点上相互交叉, (b) 支持矢量稳定在扰动下, (c) 支持矢量最多为 $+1美元, (d) 支持矢量从2到$+$+1美元的每一个矢量的矢量是可能的。 最后, 我们用一个特定类型的一般位置进行计算机模拟分析, 数据类型, 将更可能增加数据类型。