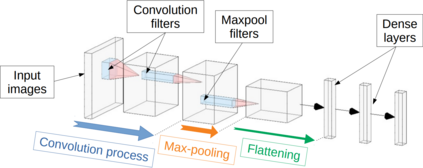
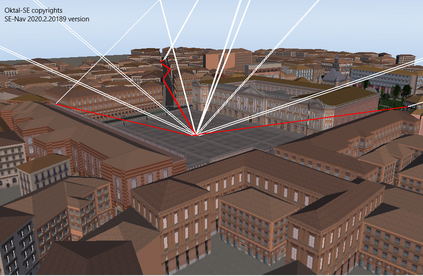
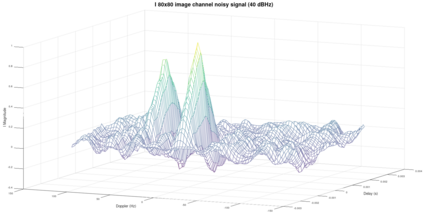
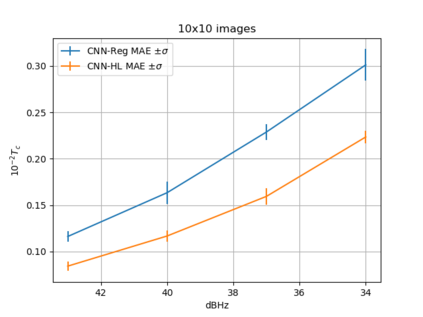
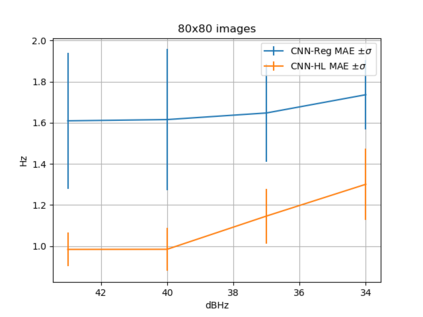
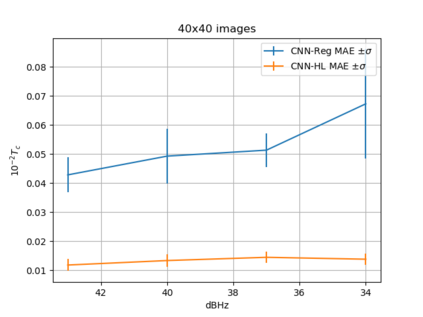
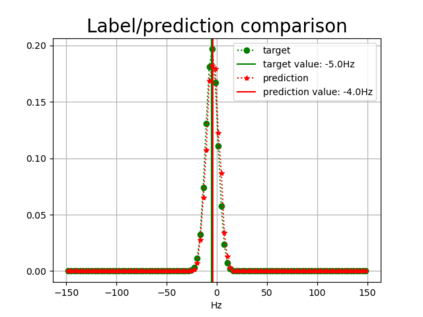
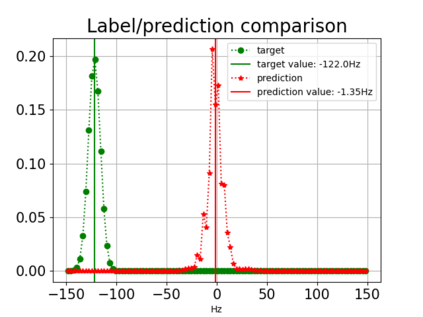
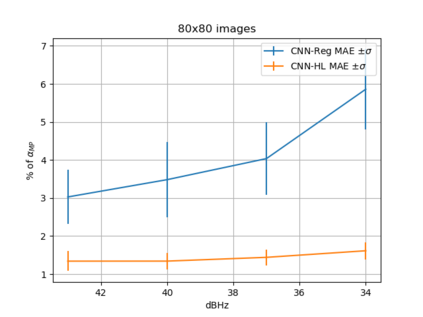
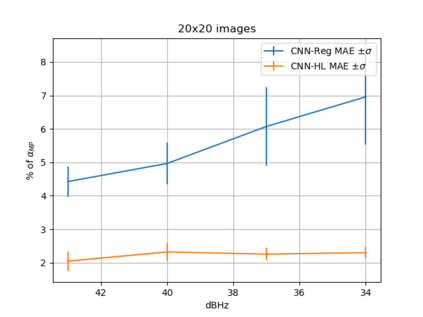
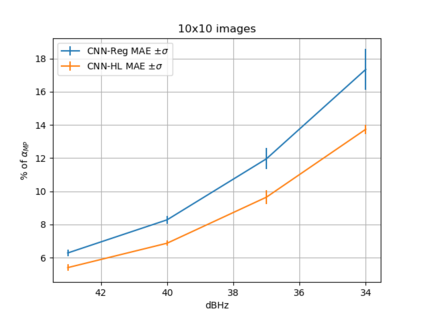
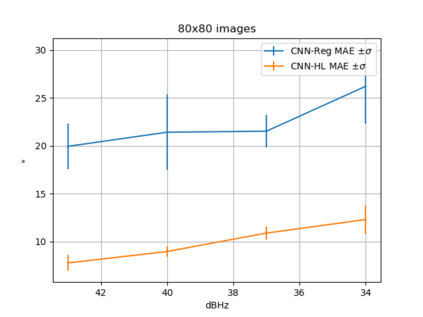
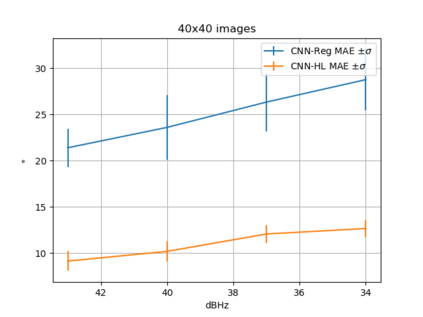
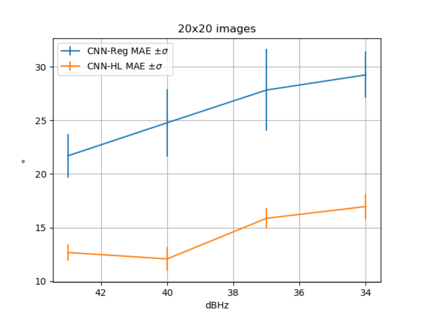
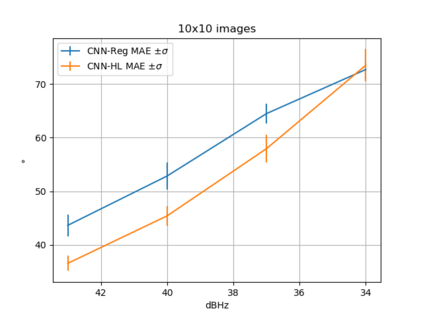
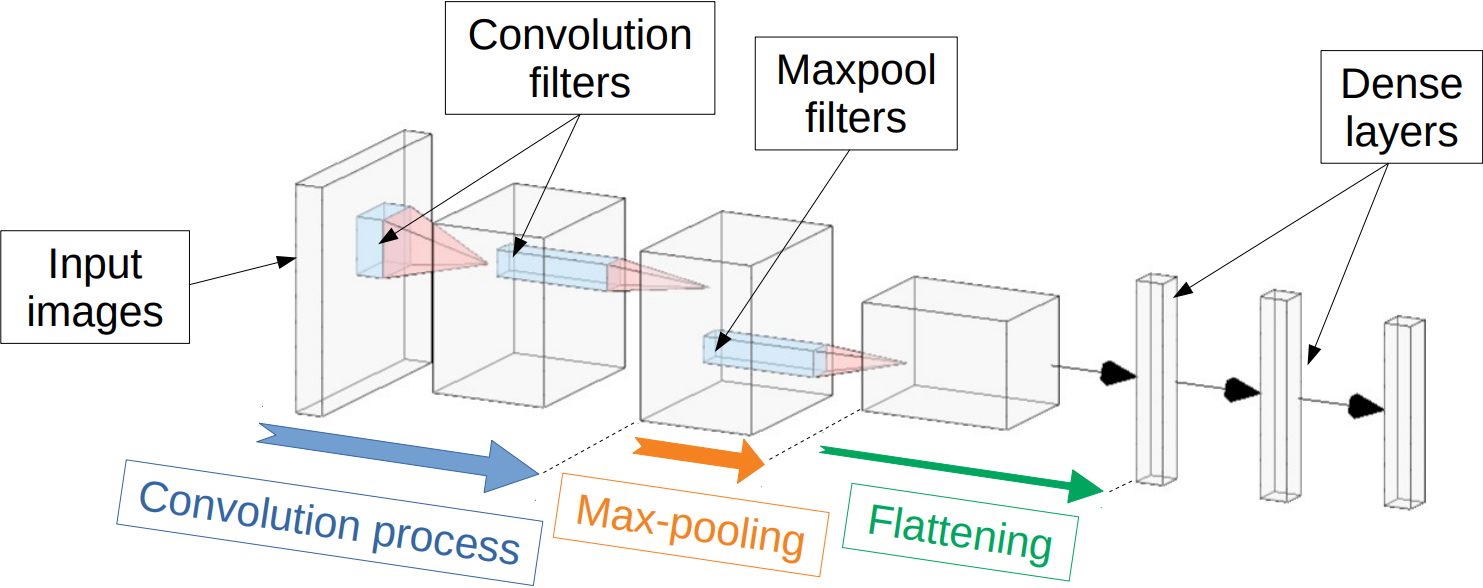
Convolutional Neural Network (CNN) have been widely used in image classification. Over the years, they have also benefited from various enhancements and they are now considered as state of the art techniques for image like data. However, when they are used for regression to estimate some function value from images, fewer recommendations are available. In this study, a novel CNN regression model is proposed. It combines convolutional neural layers to extract high level features representations from images with a soft labelling technique. More specifically, as the deep regression task is challenging, the idea is to account for some uncertainty in the targets that are seen as distributions around their mean. The estimations are carried out by the model in the form of distributions. Building from earlier work, a specific histogram loss function based on the Kullback-Leibler (KL) divergence is applied during training. The model takes advantage of the CNN feature representation and is able to carry out estimation from multi-channel input images. To assess and illustrate the technique, the model is applied to Global Navigation Satellite System (GNSS) multi-path estimation where multi-path signal parameters have to be estimated from correlator output images from the I and Q channels. The multi-path signal delay, magnitude, Doppler shift frequency and phase parameters are estimated from synthetically generated datasets of satellite signals. Experiments are conducted under various receiving conditions and various input images resolutions to test the estimation performances quality and robustness. The results show that the proposed soft labelling CNN technique using distributional loss outperforms classical CNN regression under all conditions. Furthermore, the extra learning performance achieved by the model allows the reduction of input image resolution from 80x80 down to 40x40 or sometimes 20x20.
翻译:在图像分类中广泛使用了 Convolution Neal 网络(CNN) 。 多年来, 它们也得益于各种增强, 并被视作数据等图像的艺术技术。 但是, 当它们被用于回归以估计图像的某些函数值时, 可用的建议就更少了 。 在这项研究中, 提出了一个新的CNN 回归模型 。 它结合了 convolual 神经层以软标签技术从图像中提取高层次特征表示。 更具体地说, 深软回归任务具有挑战性, 其理念是将目标中的某些不确定性视为其平均值周围的分布。 估计由40种分布方式的模型进行。 以分发方式的模型进行。 在早期工作的基础上, 基于 Kullback- Leiber (KL) 的某些特定的直方损失函数函数功能在培训中应用了。 模型利用CNN 地貌特征代表, 能够从多通道输入图像中进行估算。 模型有时用于全球导航卫星系统(GNSS) 的多路路段估算, 将多路段信号值从多路段发送的图像值向下调值输入数据, 。 在图像中, 模拟中, 将显示从链接图像的图像从链接中, 运行中, 将显示从直径解到图像的轨变换到图像的图像的轨变换成为从直径变。