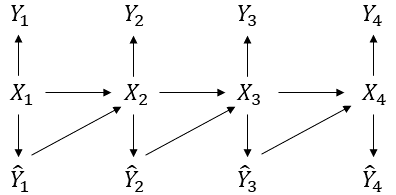
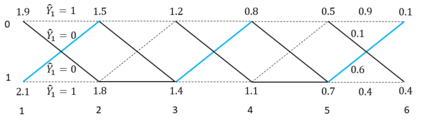
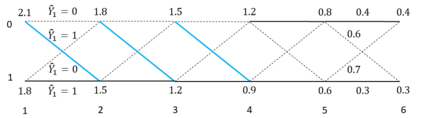
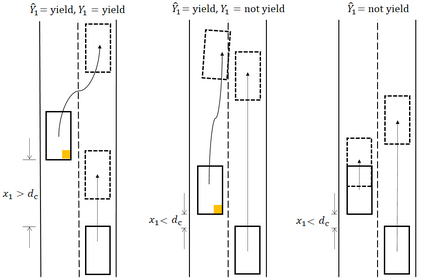
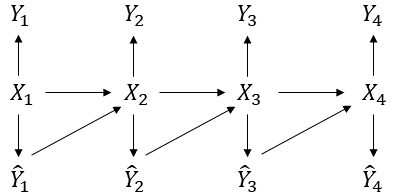
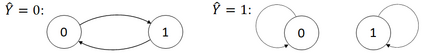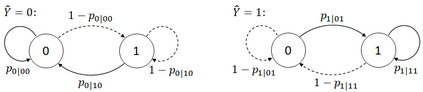Traditional statistical estimation, or statistical inference in general, is static, in the sense that the estimate of the quantity of interest does not change the future evolution of the quantity. In some sequential estimation problems however, we encounter the situation where the future values of the quantity to be estimated depend on the estimate of its current value. Examples include stock price prediction by big investors, interactive product recommendation, and behavior prediction in multi-agent systems. We may call such problems as dynamic inference. In this work, a formulation of this problem under a Bayesian probabilistic framework is given, and the optimal estimation strategy is derived as the solution to minimize the overall inference loss. How the optimal estimation strategy works is illustrated through two examples, stock trend prediction and vehicle behavior prediction. When the underlying models for dynamic inference are unknown, we can consider the problem of learning for dynamic inference. This learning problem can potentially unify several familiar machine learning problems, including supervised learning, imitation learning, and reinforcement learning.
翻译:传统的统计估计,或一般的统计推论,是静止的,也就是说,对利息数量的估计不会改变今后数量的变化。然而,在某些顺序估算问题中,我们遇到的情况是,估计数量的未来价值取决于对当前价值的估计。例子包括大投资者的股票价格预测、互动式产品建议和多试剂系统中的行为预测。我们可以称之为动态推论等问题。在这项工作中,在巴伊西亚概率框架下提出这一问题的提法,而最佳估计战略是作为尽量减少总体推论损失的解决方案产生的。最佳估计战略如何通过两个例子,即股票趋势预测和车辆行为预测来说明。当动态推论的基本模型未知时,我们可以考虑学习动态推论的问题。这一学习问题有可能将几个熟悉的机器学习问题统一起来,包括监督下的学习、模仿学习和强化学习。