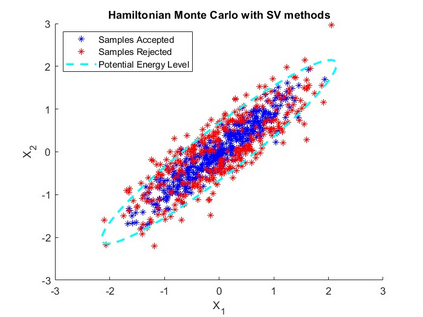
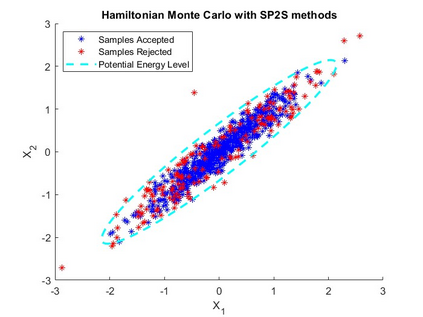
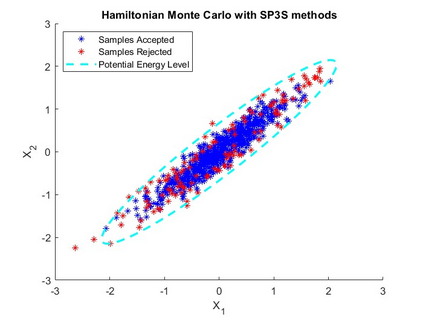
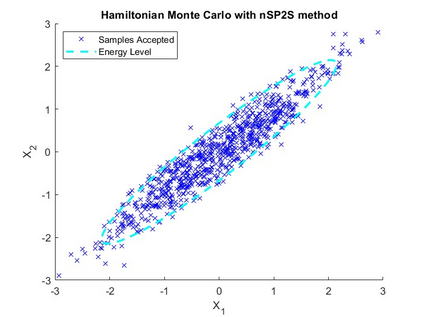
Splitting schemes are numerical integrators for Hamiltonian problems that may advantageously replace the St\"ormer-Verlet method within Hamiltonian Monte Carlo (HMC) methodology. However, HMC performance is very sensitive to the step size parameter; in this paper we propose a new method in the one-parameter family of second-order of splitting procedures that uses a well-fitting parameter that nullifies the expectation of the energy error for univariate and multivariate Gaussian distributions, taken as a problem-guide for more realistic situations; we also provide a new algorithm that through an adaptive choice of the $b$ parameter and the step-size ensures high sampling performance of HMC. For similar methods introduced in recent literature, by using the proposed step size selection, the splitting integration within HMC method never rejects a sample when applied to univariate and multivariate Gaussian distributions. For more general non Gaussian target distributions the proposed approach exceeds the principal especially when the adaptive choice is used. The effectiveness of the proposed is firstly tested on some benchmarks examples taken from literature. Then, we conduct experiments by considering as target distribution, the Log-Gaussian Cox process and Bayesian Logistic Regression.
翻译:在汉密尔顿-蒙特-蒙特-卡洛(汉密尔顿-蒙特-蒙特-卡罗(HMC))方法中,汉密尔顿问题的数字集成方案是汉密尔顿问题的数字集成器,可有利地取代St'ormer-Verlet方法。然而,HMC的性能对于步数参数参数参数非常敏感;在本文件中,我们提议在单数分解程序二阶梯组中采用新方法,使用一个适当参数,使对单数和多变数高斯分布的能源错误的期望丧失;对于更一般的非高斯目标分布,建议的办法超过了本数,特别是在采用适应性选择时;我们还提供一种新的算法,通过调适量选择美元参数和分量尺寸确保HMC的高采样性性。对于最近文献中引入的类似方法,我们采用拟议的步数选择,即步数分解方法在对单数和多变数高斯分布应用时绝不拒绝样品。对于较普通的非高斯目标分布,特别是在使用适应性选择时,拟议的办法超过了本。拟议的办法的有效性首先在从文献中对某些基准示例进行测试。然后,我们将Lo-Gsurb-regisliversisal作为目标的分布作为目标分布。我们进行实验,然后考虑将目标进行试验。