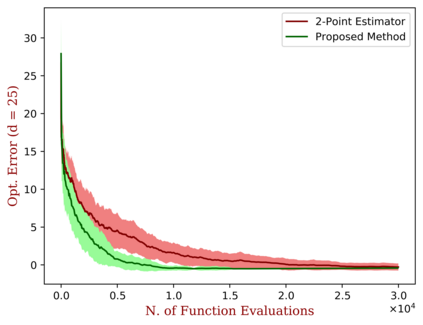
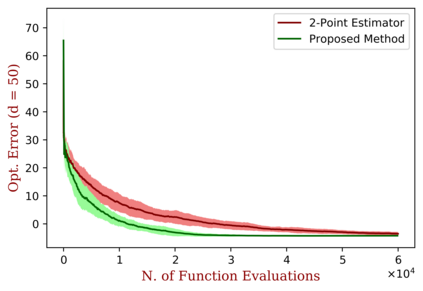
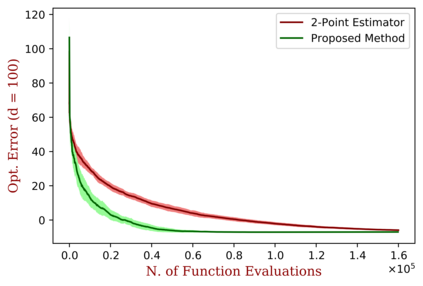
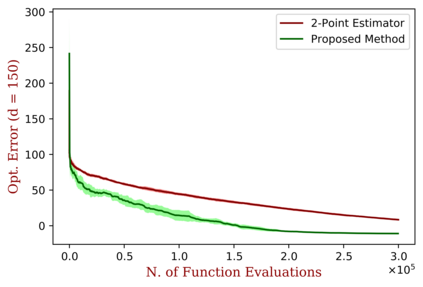
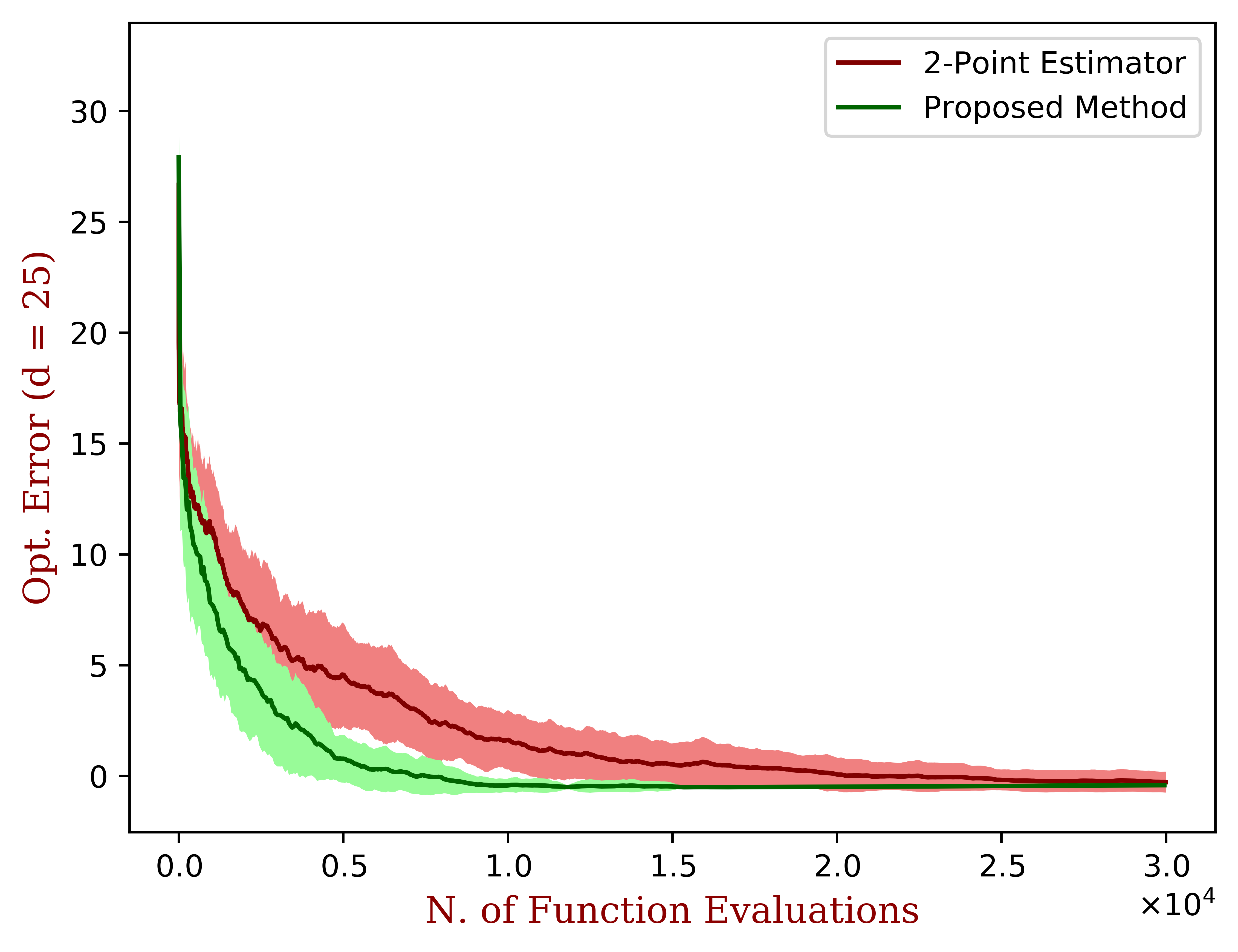
We study the problem of distributed zero-order optimization for a class of strongly convex functions. They are formed by the average of local objectives, associated to different nodes in a prescribed network of connections. We propose a distributed zero-order projected gradient descent algorithm to solve this problem. Exchange of information within the network is permitted only between neighbouring nodes. A key feature of the algorithm is that it can query only function values, subject to a general noise model, that does not require zero mean or independent errors. We derive upper bounds for the average cumulative regret and optimization error of the algorithm which highlight the role played by a network connectivity parameter, the number of variables, the noise level, the strong convexity parameter of the global objective and certain smoothness properties of the local objectives. When the bound is specified to the standard undistributed setting, we obtain an improvement over the state-of-the-art bounds, due to the novel gradient estimation procedure proposed here. We also comment on lower bounds and observe that the dependency over certain function parameters in the bound is nearly optimal.
翻译:我们研究的是,对一组强电流功能进行零顺序分配优化的问题。它们是由当地目标的平均值构成的,与指定连接网络中的不同节点相关。我们建议采用分布零顺序的预测梯度下降算法来解决这个问题。网络内部的信息交流只允许相邻节点之间进行。算法的一个关键特征是,它只能查询功能值,不受一般噪音模型的限制,而不需要零平均或独立的错误。我们从测算法的平均累积遗憾和优化误差中得出上限,该算法突出网络连通参数的作用、变量数量、噪音水平、全球目标的强共性参数以及地方目标的某些平稳性。当约束与标准的无分布环境挂钩时,我们因此处提议的新的梯度估计程序而改进了技术的状态界限。我们还评论了较低界限,并指出对约束中某些功能参数的依赖性几乎是最佳的。