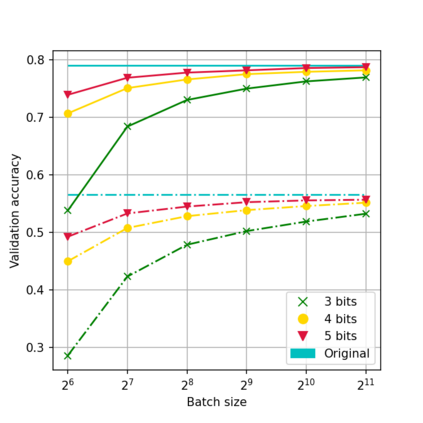
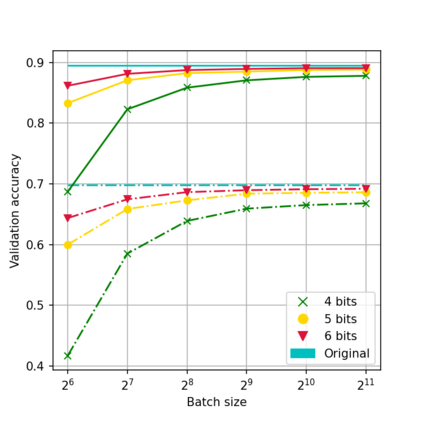
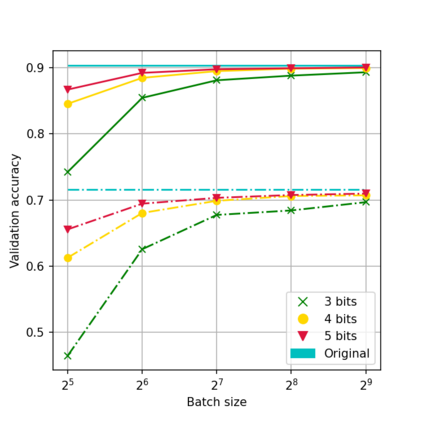
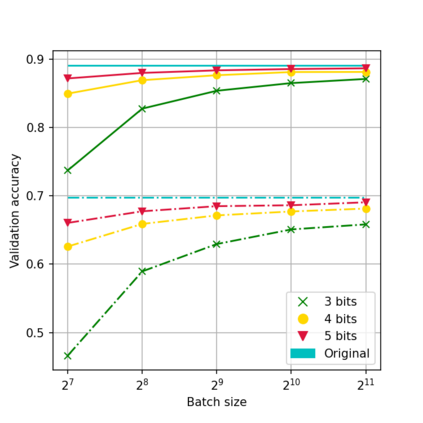
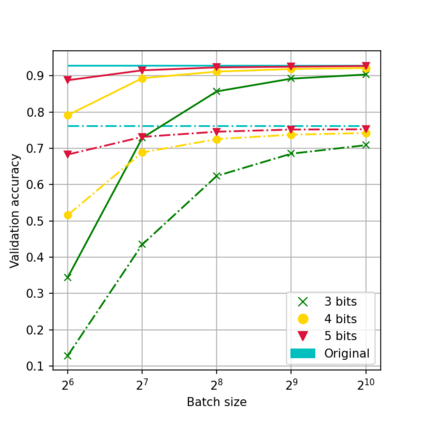
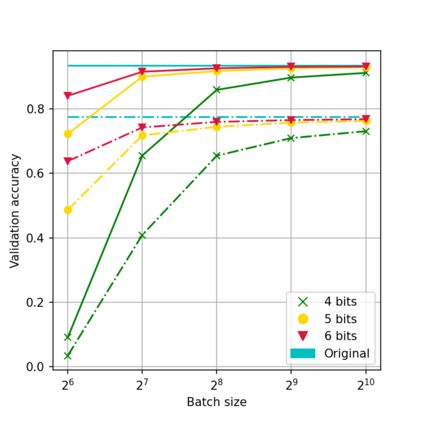
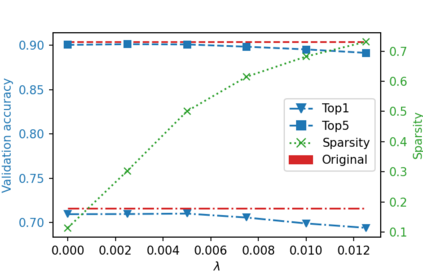
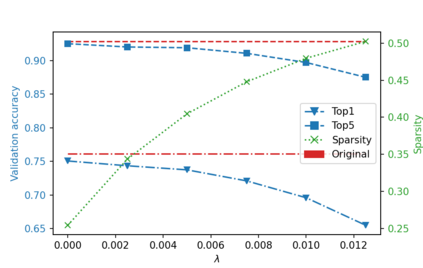
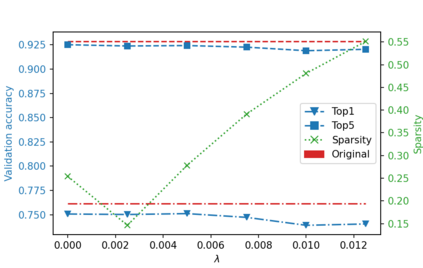
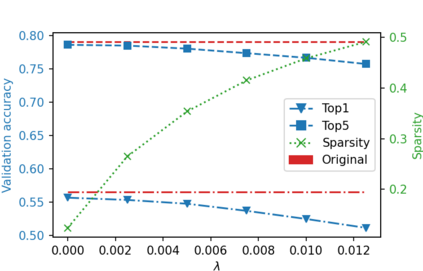
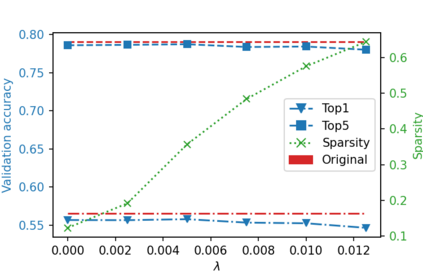
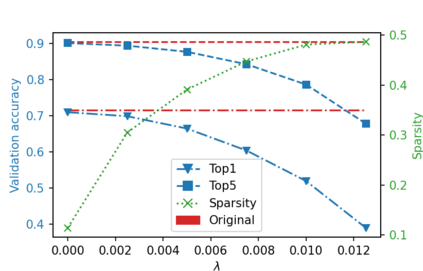
While neural networks have been remarkably successful in a wide array of applications, implementing them in resource-constrained hardware remains an area of intense research. By replacing the weights of a neural network with quantized (e.g., 4-bit, or binary) counterparts, massive savings in computation cost, memory, and power consumption are attained. To that end, we generalize a post-training neural-network quantization method, GPFQ, that is based on a greedy path-following mechanism. Among other things, we propose modifications to promote sparsity of the weights, and rigorously analyze the associated error. Additionally, our error analysis expands the results of previous work on GPFQ to handle general quantization alphabets, showing that for quantizing a single-layer network, the relative square error essentially decays linearly in the number of weights -- i.e., level of over-parametrization. Our result holds across a range of input distributions and for both fully-connected and convolutional architectures thereby also extending previous results. To empirically evaluate the method, we quantize several common architectures with few bits per weight, and test them on ImageNet, showing only minor loss of accuracy compared to unquantized models. We also demonstrate that standard modifications, such as bias correction and mixed precision quantization, further improve accuracy.
翻译:虽然神经网络在广泛的应用中取得了显著的成功,但是在资源限制的硬件中实施这些网络仍然是一个密集的研究领域。此外,我们的错误分析扩大了GPFQ以往处理一般四分化字母表的工作结果,表明对单层网络进行四分化,相对的平方错误基本上在重量数上直线衰减 -- -- 即超分化的程度。我们的结果存在于一系列投入分布中,完全相连的和进化的结构也因此扩大了先前的结果。为了对方法进行实证评估,我们量化了GPFQ以往处理一般四分化字母表的工作结果,表明对单层网络进行四分化,相对的平方错误基本上使重量数(即超分化的程度)下降。我们的结果存在于各种投入分布中,同时也是为了全面连接和进化结构,从而也扩大了先前的结果。为了对方法进行实证评估,我们量化了GPFQQ处理一般四分式字母表的工作结果,表明对于单层网络的量化,相对的正方差差差基本上使一些共同结构的精确性得到改进。