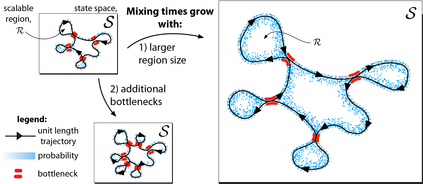
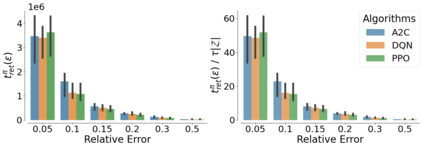
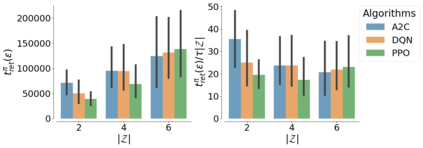
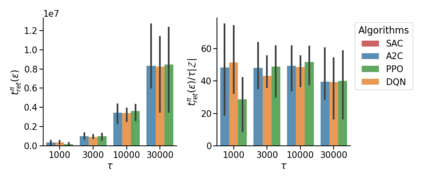
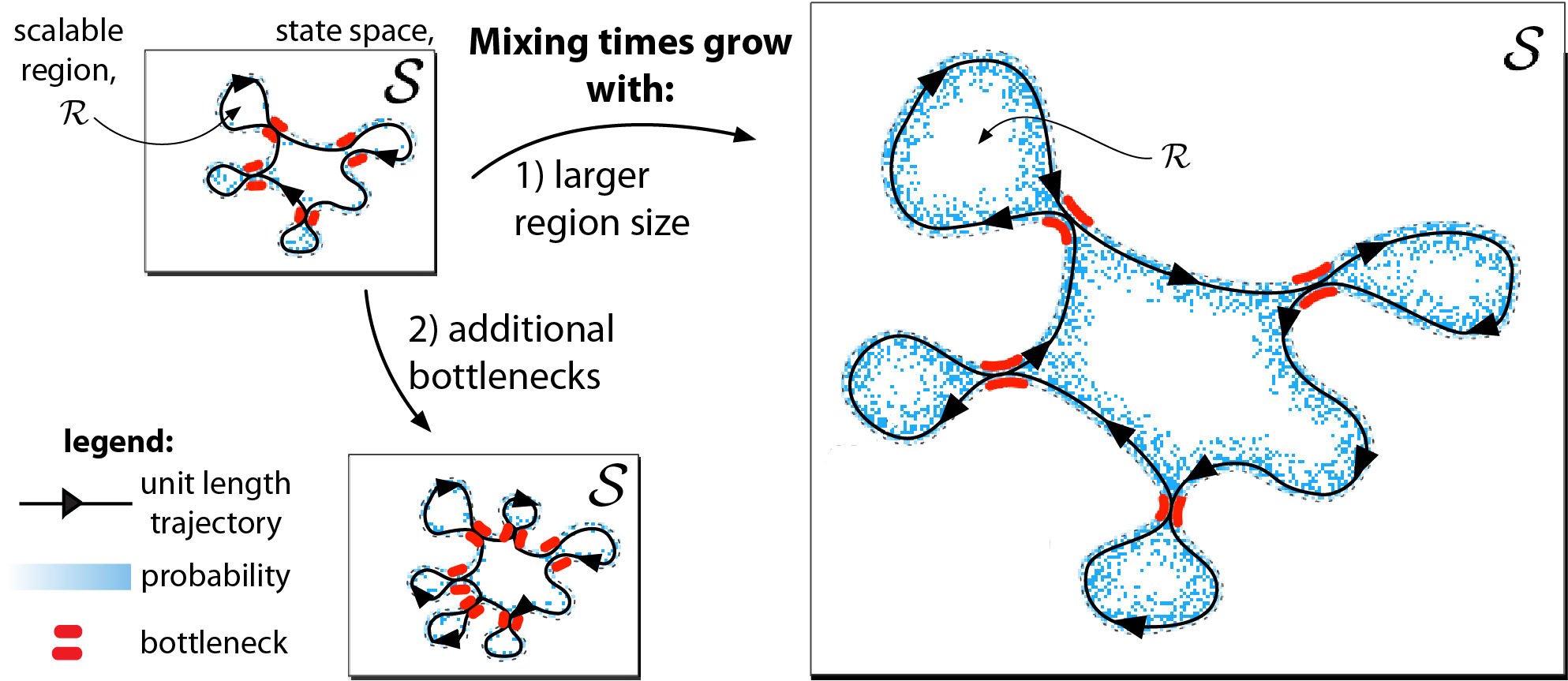
The mixing time of the Markov chain induced by a policy limits performance in real-world continual learning scenarios. Yet, the effect of mixing times on learning in continual reinforcement learning (RL) remains underexplored. In this paper, we characterize problems that are of long-term interest to the development of continual RL, which we call scalable MDPs, through the lens of mixing times. In particular, we theoretically establish that scalable MDPs have mixing times that scale polynomially with the size of the problem. We go on to demonstrate that polynomial mixing times present significant difficulties for existing approaches, which suffer from myopic bias and stale bootstrapped estimates. To validate our theory, we study the empirical scaling behavior of mixing times with respect to the number of tasks and task duration for high performing policies deployed across multiple Atari games. Our analysis demonstrates both that polynomial mixing times do emerge in practice and how their existence may lead to unstable learning behavior like catastrophic forgetting in continual learning settings.
翻译:马尔科夫链链的混合时间是由政策限制现实世界持续学习情景的绩效所引发的。然而,混合时间对持续强化学习学习(RL)的学习的影响仍未得到充分探讨。在本文中,我们通过混合时间的透镜来辨别对持续强化学习(RL)发展具有长期利益的问题,我们称之为可缩放的 MDP。特别是,我们理论上确定,可缩放的 MDP 的混合时间与问题的规模不同。我们继续表明,多元混合时间对于现有方法来说是巨大的困难,这些方法受到近似偏差和停滞的预估值的影响。为了验证我们的理论,我们研究了在多场Atari游戏中应用的高执行政策的任务和任务期限的混合时间的经验比例行为。我们的分析表明,多元混合时间在实践中确实出现,它们的存在如何导致不稳定的学习行为,例如在持续学习环境中灾难性的遗忘。
相关内容
Source: Apple - iOS 8