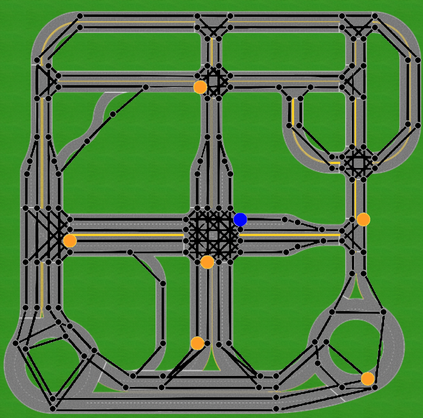
In this paper, we investigate the problem of a last-mile delivery service that selects up to $N$ available vehicles to deliver $M$ packages from a centralized depot to $M$ delivery locations. The objective of the last-mile delivery service is to jointly maximize customer satisfaction (minimize delivery time) and minimize operating cost (minimize total travel time) by selecting the optimal number of vehicles to perform the deliveries. We model this as an assignment (vehicles to packages) and path planning (determining the delivery order and route) problem, which is equivalent to the NP-hard multiple traveling salesperson problem. We propose a scalable heuristic algorithm, which sacrifices some optimality to achieve a reasonable computational cost for a high number of packages. The algorithm combines hierarchical clustering with a greedy search. To validate our approach, we compare the results of our simulation to experiments in a $1$:$25$ scale robotic testbed for future mobility systems.
翻译:在本文中,我们调查了最后英里交货服务问题,即选择最多不超过N美元的现有车辆从集中仓库向交付地点交付美元,从集中仓库向交付地点交付美元,最后英里交货服务的目标是通过选择最理想的交货车辆数量,共同最大限度地提高客户满意度(最大限度地减少交货时间)和最大限度地降低运营成本(最大限度地减少总旅行时间),我们将此模式作为分配(包裹车辆)和路径规划(确定交货订单和路线)问题,这相当于NP-硬性多重旅行销售人员问题。我们提出了一个可扩展的超电子算法,以牺牲某种最佳性,为大量交货实现合理的计算成本。这一算法将等级组合与贪婪的搜索结合起来。为了验证我们的方法,我们将我们的模拟结果与1美元:25美元的规模机器人测试床对未来的移动系统进行对比。