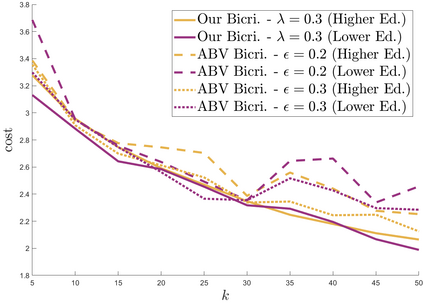
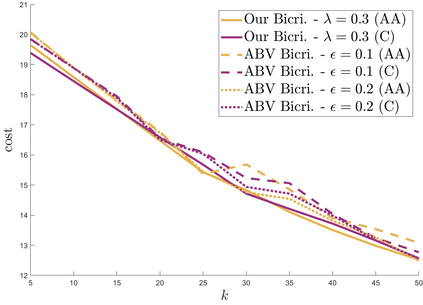
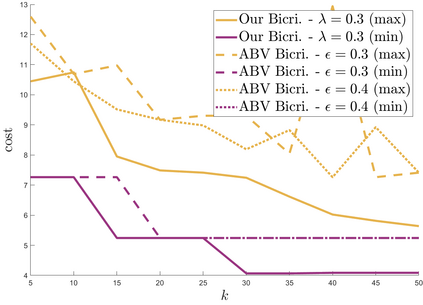
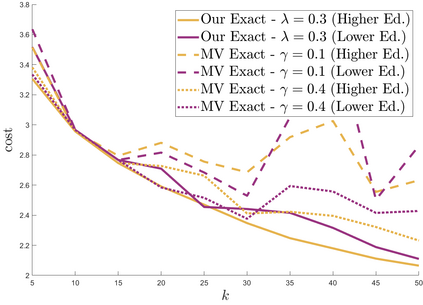
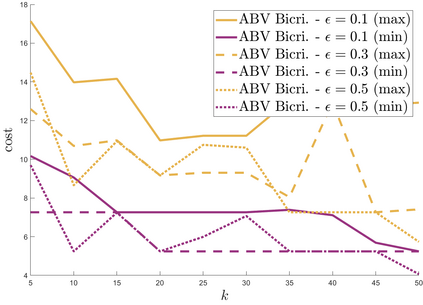
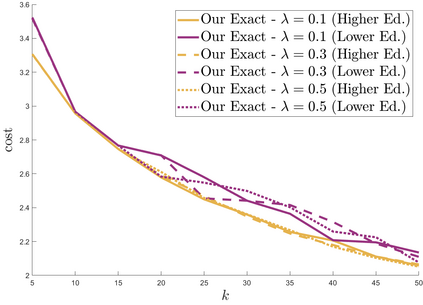
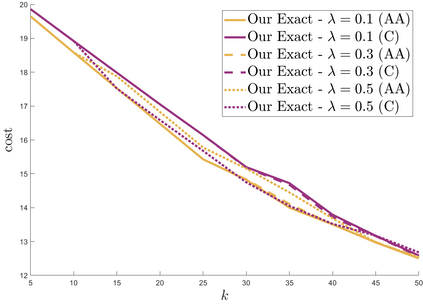
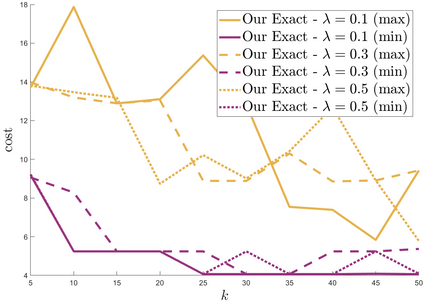
We study approximation algorithms for the socially fair $(\ell_p, k)$-clustering problem with $m$ groups, whose special cases include the socially fair $k$-median ($p=1$) and socially fair $k$-means ($p=2$) problems. We present (1) a polynomial-time $(5+2\sqrt{6})^p$-approximation with at most $k+m$ centers (2) a $(5+2\sqrt{6}+\epsilon)^p$-approximation with $k$ centers in time $n^{2^{O(p)}\cdot m^2}$, and (3) a $(15+6\sqrt{6})^p$ approximation with $k$ centers in time $k^{m}\cdot\text{poly}(n)$. The first result is obtained via a refinement of the iterative rounding method using a sequence of linear programs. The latter two results are obtained by converting a solution with up to $k+m$ centers to one with $k$ centers using sparsification methods for (2) and via an exhaustive search for (3). We also compare the performance of our algorithms with existing bicriteria algorithms as well as exactly $k$ center approximation algorithms on benchmark datasets, and find that our algorithms also outperform existing methods in practice.
翻译:我们研究社会上公平的$( ell_ p, k) 美元集中问题的近似算法与美元集团的近似算法,这些集团的特殊案例包括: 社会上公平的$- 中间美元( p=1美元) 和社会上公平的美元( 美元=2美元) 美元( p=2美元) 问题。 我们展示了 (1) 美元( 5+2\ sqrt{ 6}) p$- 同意美元( 最多 $+美元) 中心 (2) 美元( 5+2\ sqrt{ 6 ⁇ eepsilon) 美元( p) 美元与美元( 美元) 美元( 美元/ 美元) 美元( 美元) 和美元( 美元) 美元( 美元) 美元( 美元), 美元( 美元) 和美元( 美元) 美元( ) 美元( ) 美元( ) 美元( ) 美元( ) 美元( ) ( 美元) ( ) ( 美元( 美元) ( ) ( 美元) ( 美元) ( 美元) ( ) ( ) ( ) ( 美元) ( ) ( 美元) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 美元) (