A class of Finite difference Methods for solving inhomogeneous damped wave equations

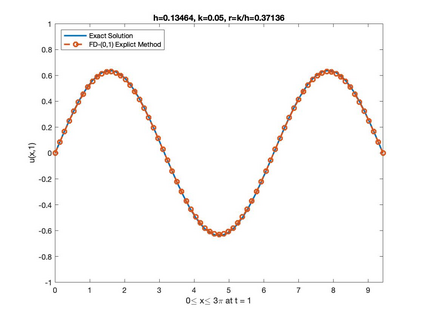
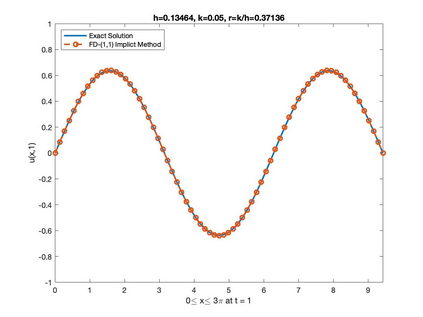
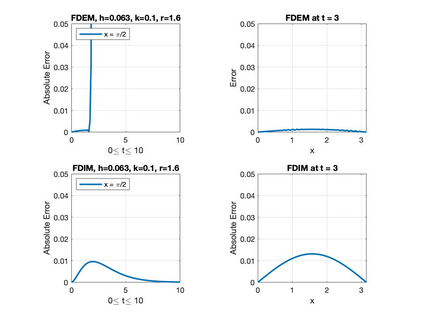
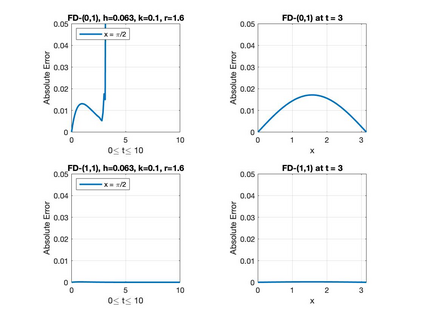
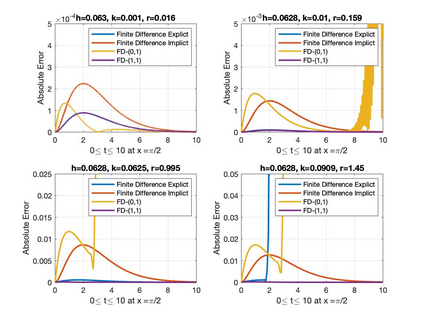
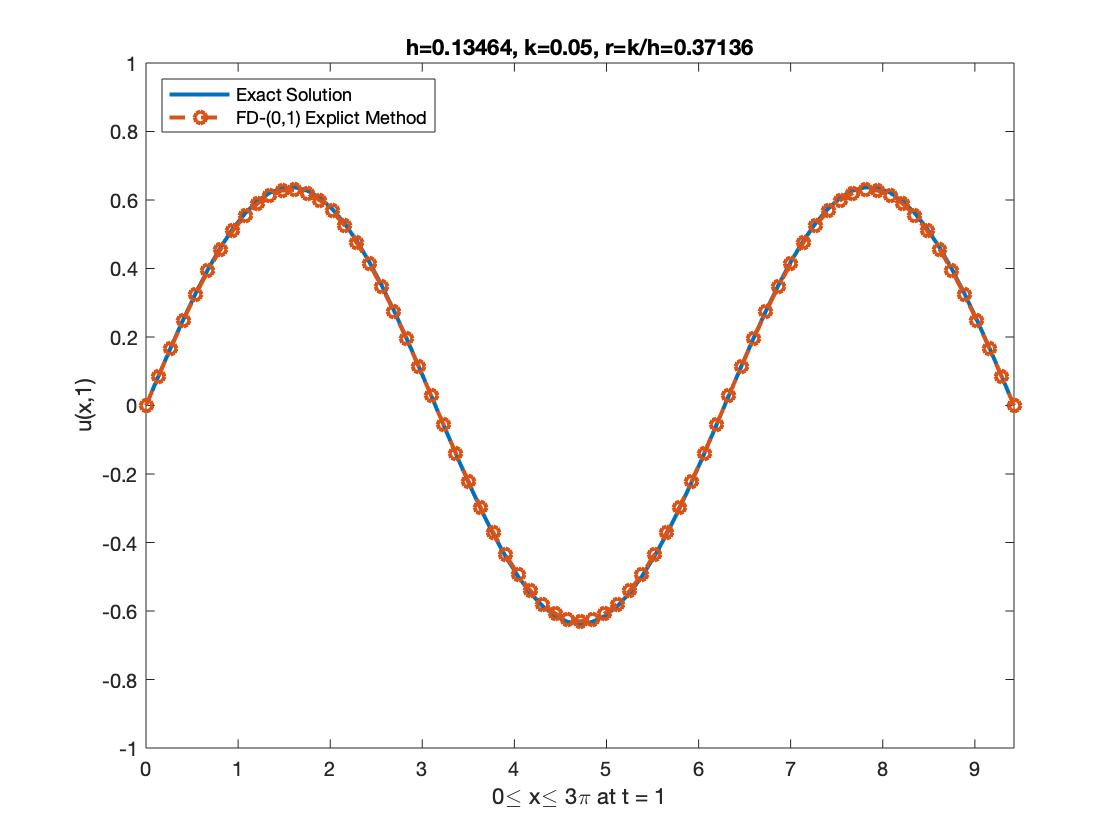
In this paper, a class of finite difference numerical techniques is presented to solve the second-order linear inhomogeneous damped wave equation. The consistency, stability, and convergences of these numerical schemes are discussed. The results obtained are compared to the exact solution, ordinary explicit, implicit finite difference methods, and the fourth-order compact method (FOCM). The general idea of these methods is developed by using the C0-semigroups operator theory. We also showed that the stability region for the explicit finite difference scheme depends on the damping coefficient.