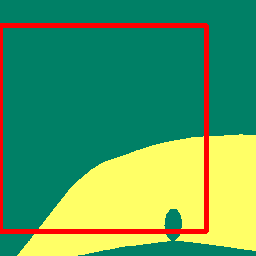
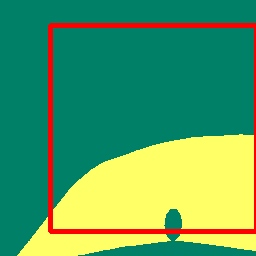
We survey the mathematical foundations of geometric deep learning, focusing on group equivariant and gauge equivariant neural networks. We develop gauge equivariant convolutional neural networks on arbitrary manifolds $\mathcal{M}$ using principal bundles with structure group $K$ and equivariant maps between sections of associated vector bundles. We also discuss group equivariant neural networks for homogeneous spaces $\mathcal{M}=G/K$, which are instead equivariant with respect to the global symmetry $G$ on $\mathcal{M}$. Group equivariant layers can be interpreted as intertwiners between induced representations of $G$, and we show their relation to gauge equivariant convolutional layers. We analyze several applications of this formalism, including semantic segmentation and object detection networks. We also discuss the case of spherical networks in great detail, corresponding to the case $\mathcal{M}=S^2=\mathrm{SO}(3)/\mathrm{SO}(2)$. Here we emphasize the use of Fourier analysis involving Wigner matrices, spherical harmonics and Clebsch-Gordan coefficients for $G=\mathrm{SO}(3)$, illustrating the power of representation theory for deep learning.
翻译:我们调查了几何深层学习的数学基础, 重点是组等离子值和测量等离异性神经网络。 我们开发关于任意的元体的测量等离异共变神经网络 $\ mathcal{M} 我们使用结构组的主要捆绑 $K$ 和相关矢量捆绑各部分之间的等异地图 。 我们还讨论同质空间的群异异性神经网络 $\ mathcal{M} /K$, 而不是全球对等性$G$的对等性 。 集团等异性神经网络可以被解释为 $G$ 的诱导代表之间的双向关系, 我们展示了它们与等异性共振图层结构的关系 。 我们分析了这种形式主义的一些应用, 包括语系分解和对象探测网络。 我们还详细讨论了球体网络的例子, 与 $\mathcal=mall{Metrial{ { mathmas} (3)/\ matricalSOral=2美元。 这里我们强调使用四SOSOILSOILSOILSOILSOIL 。