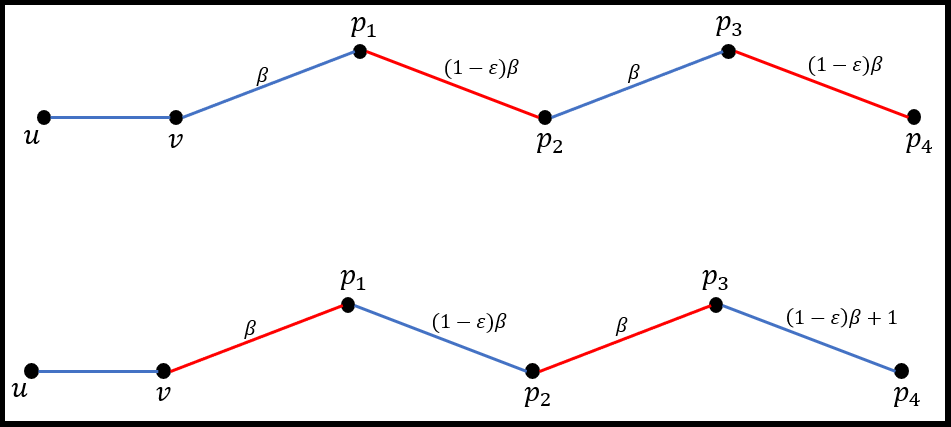
In their breakthrough ICALP'15 paper, Bernstein and Stein presented an algorithm for maintaining a $(3/2+\epsilon)$-approximate maximum matching in fully dynamic {\em bipartite} graphs with a {\em worst-case} update time of $O_\epsilon(m^{1/4})$; we use the $O_\epsilon$ notation to suppress the $\epsilon$-dependence. Their main technical contribution was in presenting a new type of bounded-degree subgraph, which they named an {\em edge degree constrained subgraph (EDCS)}, which contains a large matching -- of size that is smaller than the maximum matching size of the entire graph by at most a factor of $3/2+\epsilon$. They demonstrate that the EDCS can be maintained with a worst-case update time of $O_\epsilon(m^{1/4})$, and their main result follows as a direct corollary. In their followup SODA'16 paper, Bernstein and Stein generalized their result for general graphs, achieving the same update time of $O_\epsilon(m^{1/4})$, albeit with an amortized rather than worst-case bound. To date, the best {\em deterministic} worst-case update time bound for {\em any} better-than-2 approximate matching is $O(\sqrt{m})$ [Neiman and Solomon, STOC'13], [Gupta and Peng, FOCS'13]; allowing randomization (against an oblivious adversary) one can achieve a much better (still polynomial) update time for approximation slightly below 2 [Behnezhad, Lacki and Mirrokni, SODA'20]. In this work we\footnote{\em quasi nanos, gigantium humeris insidentes} simplify the approach of Bernstein and Stein for bipartite graphs, which allows us to generalize it for general graphs while maintaining the same bound of $O_\epsilon(m^{1/4})$ on the {\em worst-case} update time. Moreover, our approach is {\em density-sensitive}: If the {\em arboricity} of the dynamic graph is bounded by $\alpha$ at all times, then the worst-case update time of the algorithm is $O_\epsilon(\sqrt{\alpha})$.
翻译:Bernstein and Stein在他们的CricalP'15的突破性论文中展示了一种算法, 用于保持美元( 3/2 ⁇ epsilon) $( 3/2 ⁇ epsilon) 的最大匹配值, 在完全动态的2 biparte} 图形中, 以最坏的情况更新 $( ⁇ epsilon) (m}1/4} 美元; 我们使用美元表示的提示值来压制美元( 美元) 的依赖性。 他们的主要技术贡献在于展示一种新的约束性子( 20级) 平面分层( EDCS ), 包含一个巨大的匹配值 -- 大于整个图表的最大匹配值的大小, 3/2 ⁇ epsilon (m) 更新 美元( 0. 1/4} 以最坏的情况更新 以我们最坏的时序( ) 以平面的平面( ) 平面( 平面) 平面( 平面) 更新一个最坏的时段时间( )