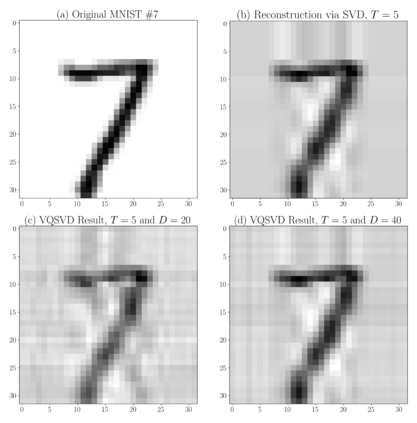
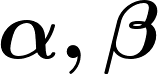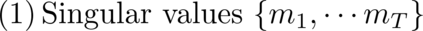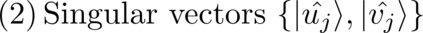Singular value decomposition is central to many problems in engineering and scientific fields. Several quantum algorithms have been proposed to determine the singular values and their associated singular vectors of a given matrix. Although these algorithms are promising, the required quantum subroutines and resources are too costly on near-term quantum devices. In this work, we propose a variational quantum algorithm for singular value decomposition (VQSVD). By exploiting the variational principles for singular values and the Ky Fan Theorem, we design a novel loss function such that two quantum neural networks (or parameterized quantum circuits) could be trained to learn the singular vectors and output the corresponding singular values. Furthermore, we conduct numerical simulations of VQSVD for random matrices as well as its applications in image compression of handwritten digits. Finally, we discuss the applications of our algorithm in recommendation systems and polar decomposition. Our work explores new avenues for quantum information processing beyond the conventional protocols that only works for Hermitian data, and reveals the capability of matrix decomposition on near-term quantum devices.
翻译:单值分解是工程和科学领域许多问题的核心。 几个量子算法已被提出来确定某个矩阵的单值及其相关的单向矢量。 虽然这些算法很有希望, 但所需的量子路程和资源在近期量子装置上费用太高。 在这项工作中, 我们提出了单值分解的变量算法( VQSVD ) 。 通过利用单值和 Ky Fan Theorem 的变异原则, 我们设计了一个新的损失函数, 使两个量子神经网络( 或参数化量子电路) 能够接受培训, 学习单向矢量矢量和输出相应的单向值。 此外, 我们还对随机矩阵进行VQSVD的数值模拟, 以及将其应用于手写数字的图像压缩。 最后, 我们讨论我们的算法在建议系统和极分解配置中的应用。 我们的工作探索了超出常规协议的量子信息处理的新途径, 只对赫米提亚数据有效, 并展示了在近期量子装置上矩阵分解的能力 。