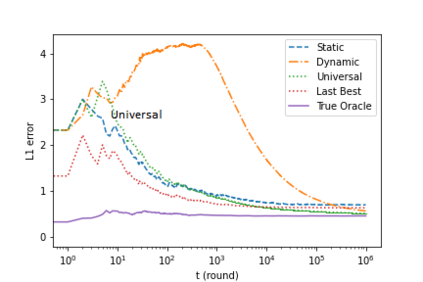
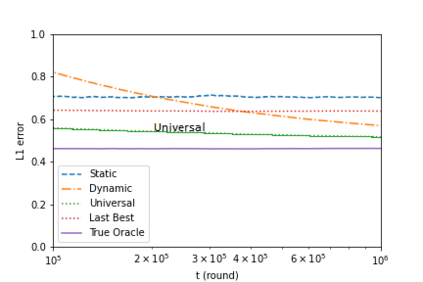
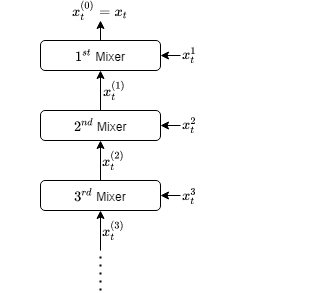
We introduce an online convex optimization algorithm which utilizes projected subgradient descent with optimal adaptive learning rates. Our method provides second-order minimax-optimal dynamic regret guarantee (i.e. dependent on the sum of squared subgradient norms) for a sequence of general convex functions, which may not have strong convexity, smoothness, exp-concavity or even Lipschitz-continuity. The regret guarantee is against any comparator decision sequence with bounded path variation (i.e. sum of the distances between successive decisions). We generate the lower bound of the worst-case second-order dynamic regret by incorporating actual subgradient norms. We show that this lower bound matches with our regret guarantee within a constant factor, which makes our algorithm minimax optimal. We also derive the extension for learning in each decision coordinate individually. We demonstrate how to best preserve our regret guarantee in a truly online manner, when the bound on path variation of the comparator sequence grows in time or the feedback regarding such bound arrives partially as time goes on. We further build on our algorithm to eliminate the need of any knowledge on the comparator path variation, and provide minimax optimal second-order regret guarantees with no a priori information. Our approach can compete against all comparator sequences simultaneously (universally) in a minimax optimal manner, i.e. each regret guarantee depends on the respective comparator path variation. We discuss modifications to our approach which address complexity reductions for time, computation and memory. We further improve our results by making the regret guarantees also dependent on comparator sets' diameters in addition to the respective path variations.
翻译:我们引入了一个在线 convex 优化算法, 使用预测的亚梯度下降, 并优化适应性学习率。 我们的方法为一般 convex 函数序列提供了第二阶次的最小最大最优化动态遗憾保证( 取决于平方次梯度规范之和 ), 它可能没有很强的共振、 光滑、 Exp- concavity 甚至是利普西茨- continuality 。 我们的遗憾保证是, 任何参照方选择序列的路径都存在受约束路径变异( 即相继决定之间的距离之和 ) 。 我们的方法通过纳入实际的次梯度规范, 产生最差的第二阶次最优化的动态遗憾。 我们显示,这种与我们的后悔保证的较低约束匹配在一个不变因素中, 使我们的算法最优化。 我们还在每项决定的单个协调中进行扩展。 我们展示如何以真正的在线方式最好地保持我们的遗憾保证。 当参照方序列的路径变异性在时间增加, 或关于这种变异于时间。 我们进一步利用我们的第二个算法来消除任何关于比较国程前级路径上的任何知识, 在前比较国的变变, 我们的排序中, 也提供我们最优级次的排序的递减。