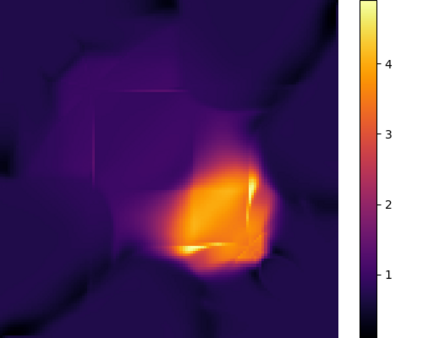
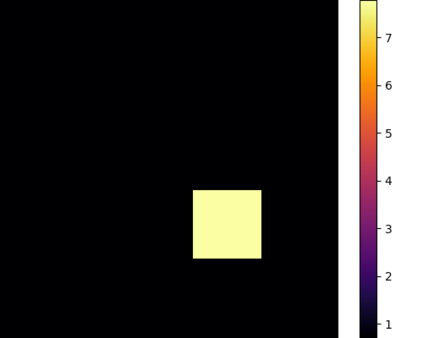
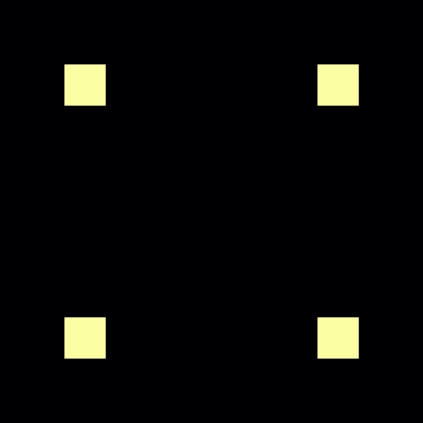
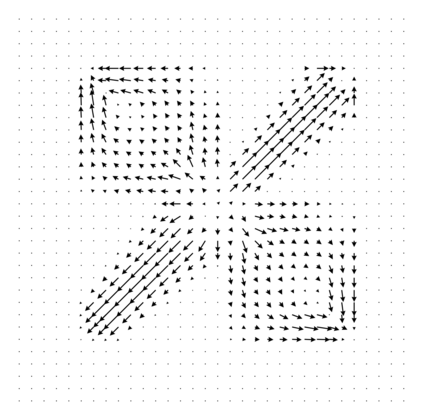
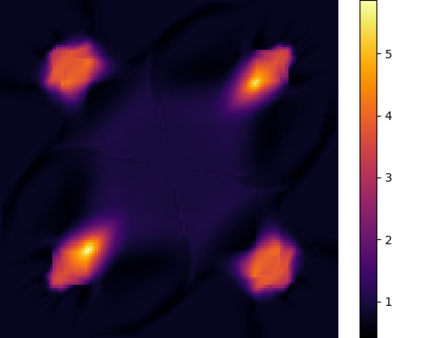
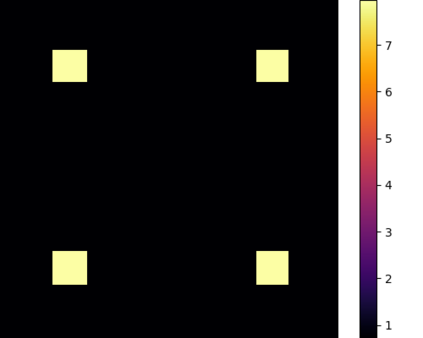
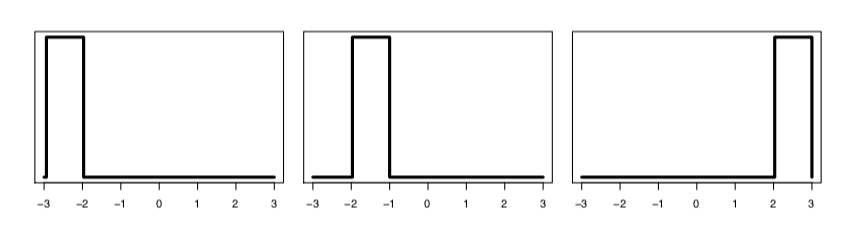
We study the problem of optimal transport in tropical geometry and define the Wasserstein-$p$ distances in the continuous metric measure space setting of the tropical projective torus. We specify the tropical metric -- a combinatorial metric that has been used to study of the tropical geometric space of phylogenetic trees -- as the ground metric and study the cases of $p=1,2$ in detail. The case of $p=1$ gives an efficient computation of the infinitely-many geodesics on the tropical projective torus, while the case of $p=2$ gives a form for Fr\'{e}chet means and a general inner product structure. Our results also provide theoretical foundations for geometric insight a statistical framework in a tropical geometric setting. We construct explicit algorithms for the computation of the tropical Wasserstein-1 and 2 distances and prove their convergence. Our results provide the first study of the Wasserstein distances and optimal transport in tropical geometry. Several numerical examples are provided.
翻译:我们研究热带几何的最佳运输问题,并在热带投影体连续计量空间设置中界定瓦塞斯坦-1美元距离。我们把热带指标 -- -- 用于研究热带植物树的热带几何空间的组合度度度 -- -- 作为地面指标,详细研究1,2美元的个案。美元=1美元的个案对热带投影体上无限多的大地测量进行了高效计算,而美元=2美元的个案为Fr\{{echet手段和一般内部产品结构提供了一种形式。我们的结果也为几何观察提供了理论基础,在热带几何环境中形成一个统计框架。我们为计算热带瓦塞斯坦-1和2个距离并证明其趋同性,我们的结果提供了瓦塞斯坦距离和热带几何学中最佳运输的首次研究。我们提供了几个数字例子。