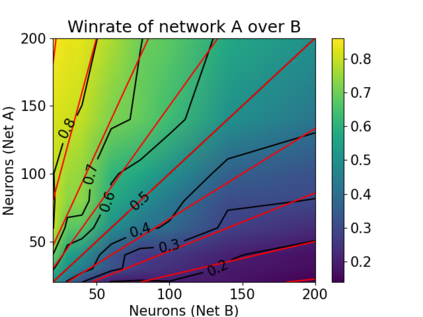
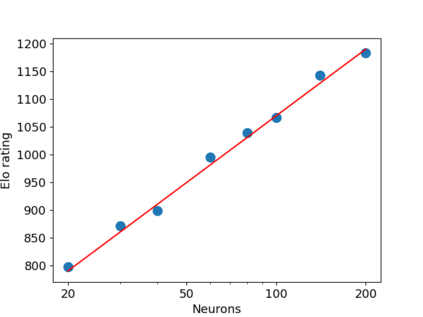
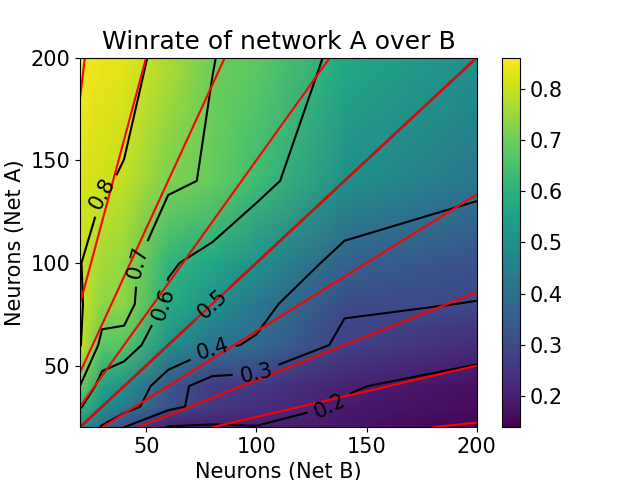
Natural selection drives species to develop brains, with sizes that increase with the complexity of the tasks to be tackled. Our goal is to investigate the balance between the metabolic costs of larger brains compared to the advantage they provide in solving general and combinatorial problems. Defining advantage as the performance relative to competitors, a two-player game based on the knapsack problem is used. Within this framework, two opponents compete over shared resources, with the goal of collecting more resources than the opponent. Neural nets of varying sizes are trained using a variant of the AlphaGo Zero algorithm. A surprisingly simple relation, $N_A/(N_A+N_B)$, is found for the relative win rate of a net with $N_A$ neurons against one with $N_B$. Success increases linearly with investments in additional resources when the networks sizes are very different, i.e. when $N_A \ll N_B$, with returns diminishing when both networks become comparable in size.
翻译:自然选择驱使物种开发大脑, 其规模随着要处理的任务的复杂性而增加。 我们的目标是调查较大大脑的代谢成本与其在解决一般问题和组合问题方面提供的优势之间的平衡。 将优势定义为相对于竞争者的绩效, 使用基于 knapsack 问题的双人游戏。 在此框架内, 两位对手争夺共享资源, 目标是收集比对手更多的资源。 使用 AlphaGo Zero 算法变量对不同尺寸的神经网进行了培训。 一个惊人的简单关系, 即$_A/ (N_A+N_B), 与 $N 和 $N_B 相对的神经元相对赢利率相当。 当网络规模非常不同时, 即$N_A\ ll N_B$, 成功随着对额外资源的投资, 即当两个网络的规模相似时回报减少时, 成功率会直线增长。