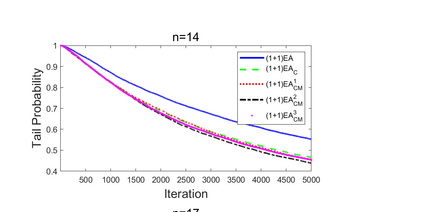
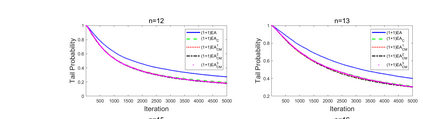
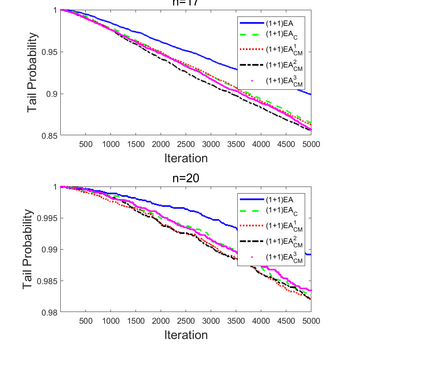
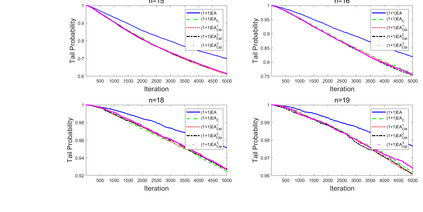
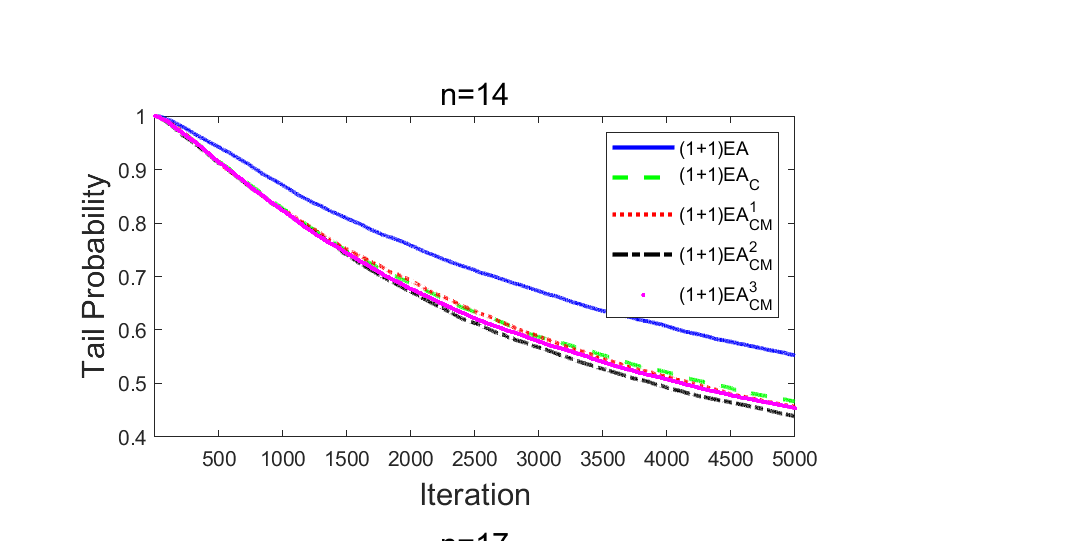
Although differential evolution (DE) algorithms perform well on a large variety of complicated optimization problems, only a few theoretical studies are focused on the working principle of DE algorithms. To make the first attempt to reveal the function of binomial crossover, this paper aims to answer whether it can reduce the approximation error of evolutionary algorithms. By investigating the expected approximation error and the probability of not finding the optimum, we conduct a case study comparing two evolutionary algorithms with and without binomial crossover on two classical benchmark problems: OneMax and Deceptive. It is proven that using binomial crossover leads to the dominance of transition matrices. As a result, the algorithm with binomial crossover asymptotically outperforms that without crossover on both OneMax and Deceptive, and outperforms on OneMax, however, not on Deceptive. Furthermore, an adaptive parameter strategy is proposed which can strengthen the superiority of binomial crossover on Deceptive.
翻译:虽然差异进化(DE)算法在一系列复杂的优化问题上效果良好,但只有少数理论研究侧重于DE算法的工作原理。为了首次尝试揭示二进制交叉的功能,本文件旨在回答它是否能够减少进化算法近似错误。通过调查预期近似错误和找不到最佳的概率,我们进行了一项案例研究,将两种进化算法与两个典型基准问题(一氧化物和欺骗性)的二进制交叉比较,而不是二进制交叉比较。事实证明,使用二进制交叉法可以导致过渡矩阵的主导地位。结果就是,二进制交叉交错的算法,在不跨越一氧化物和欺骗性两者的情况下,超越了OneMAx。此外,我们提出了一个适应参数战略,可以加强二进制交叉在欺骗性上的优势。