Broken Neural Scaling Laws

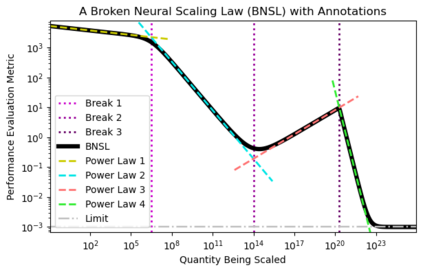
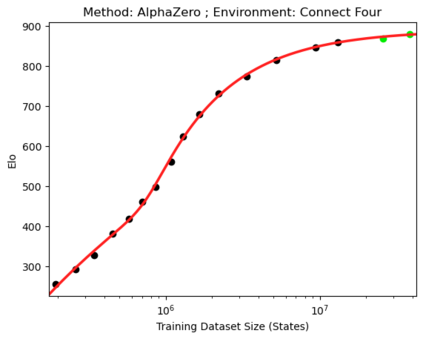
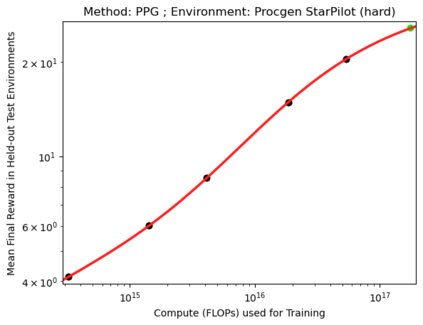
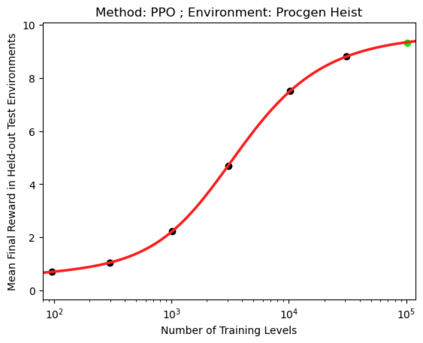
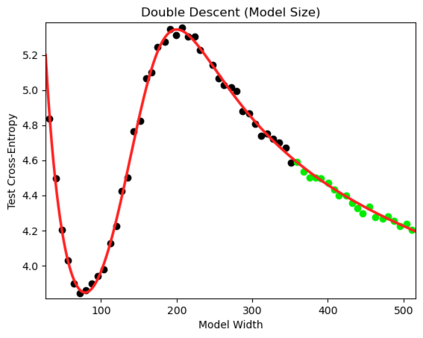
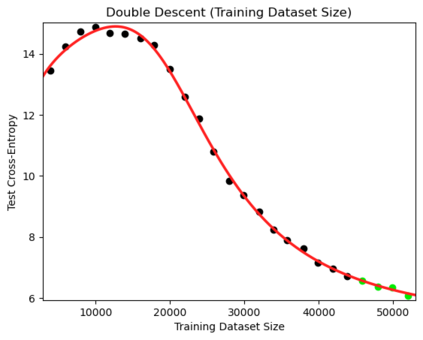
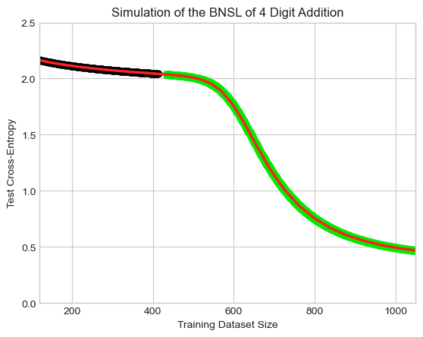
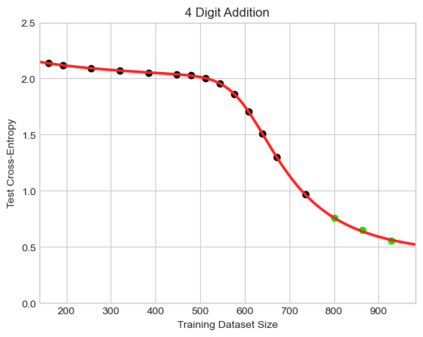
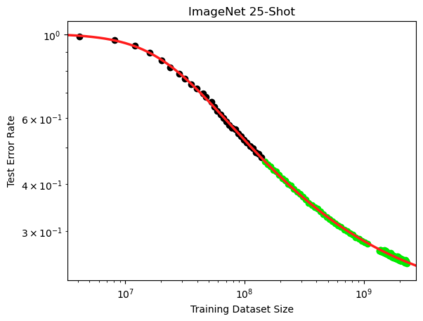
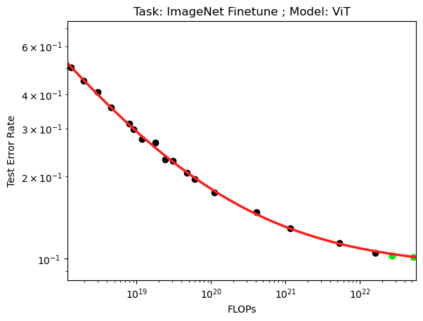
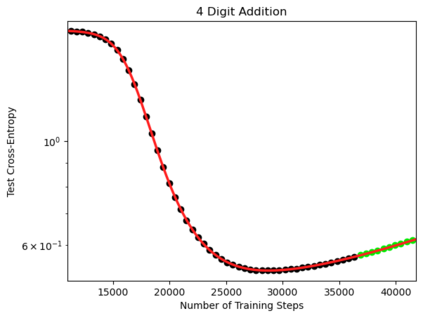
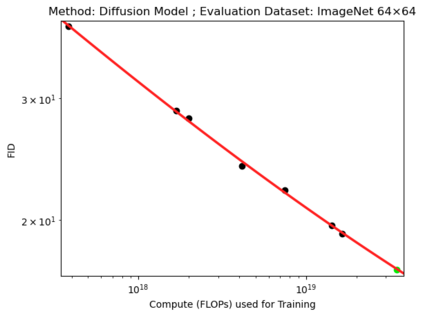
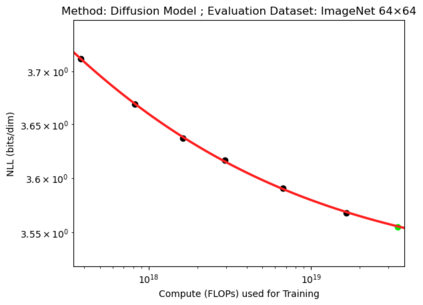
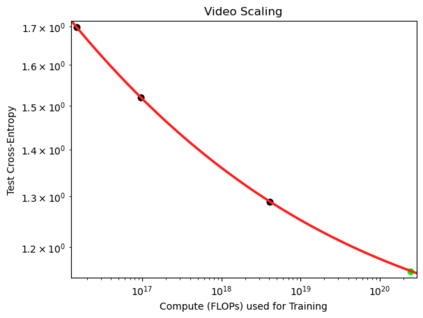
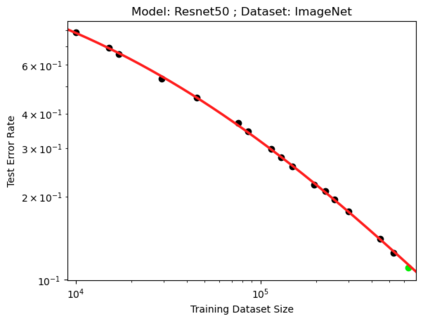
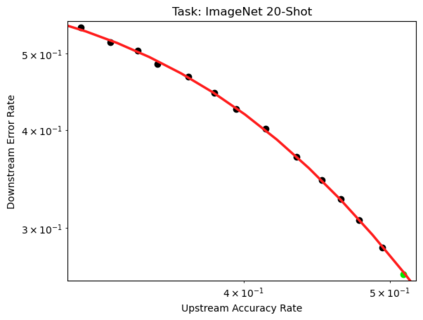
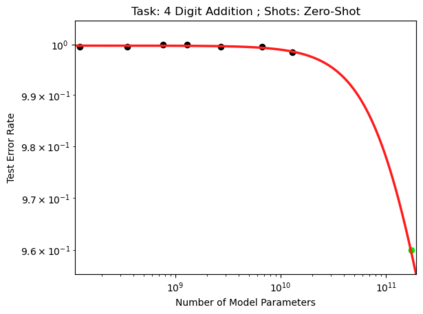
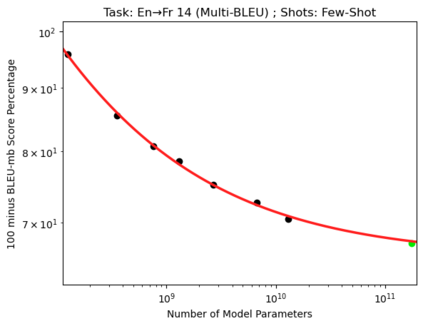
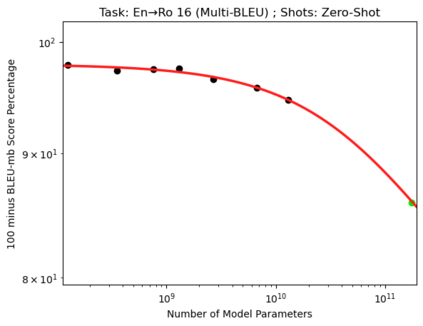
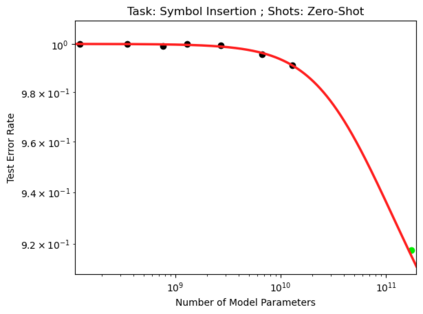
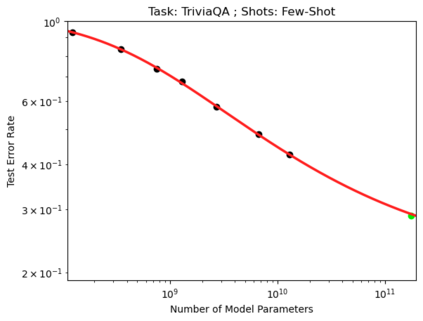
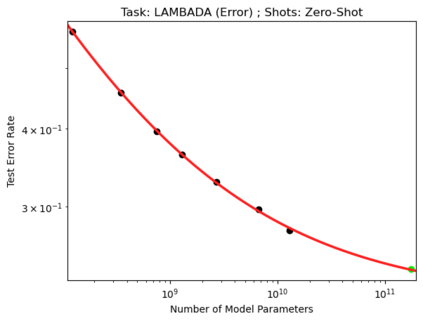
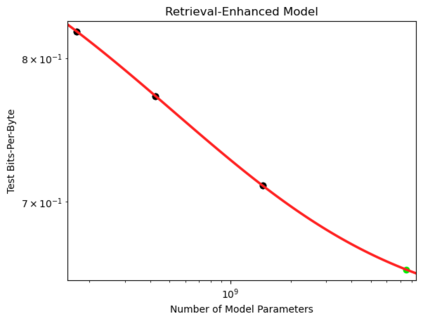
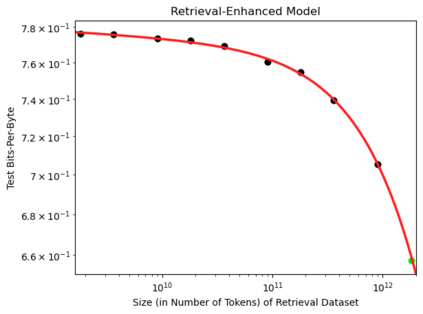
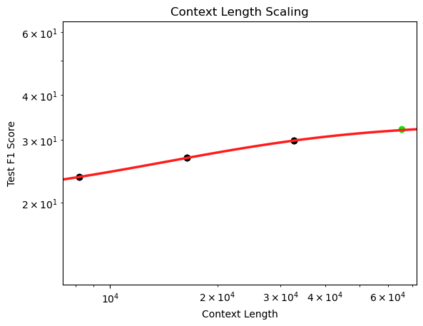
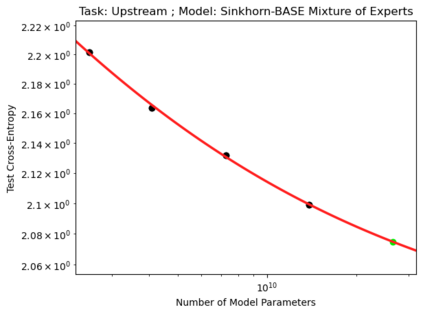
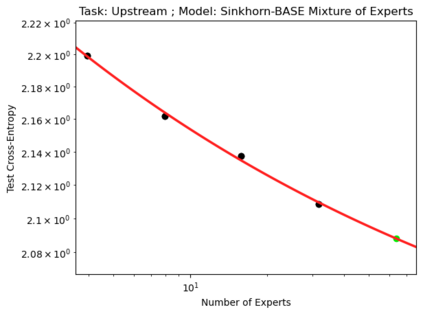
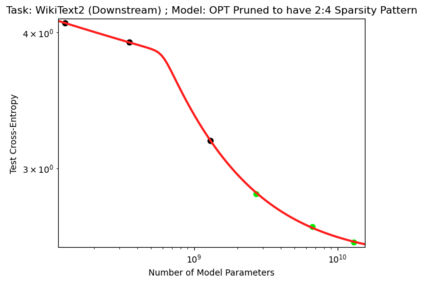
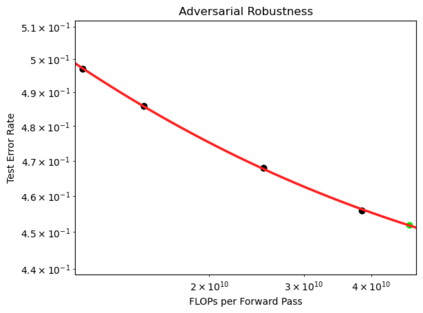
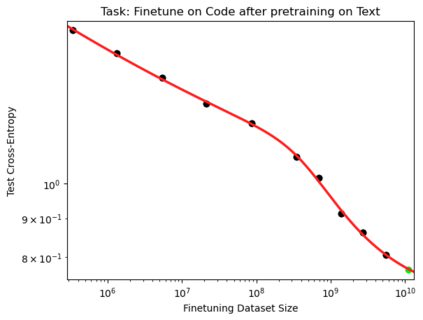
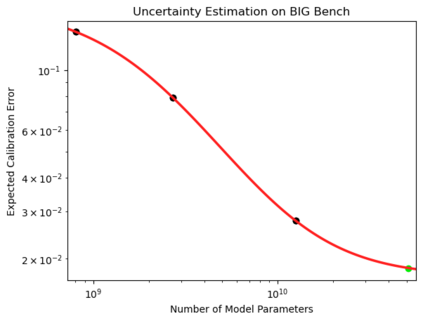
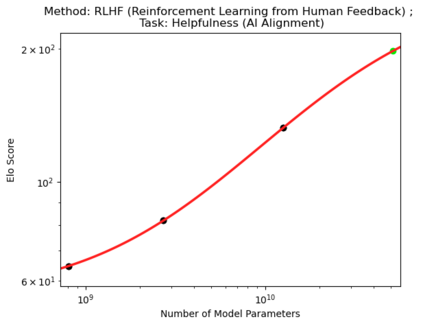
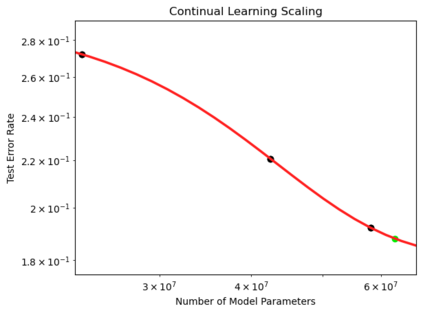
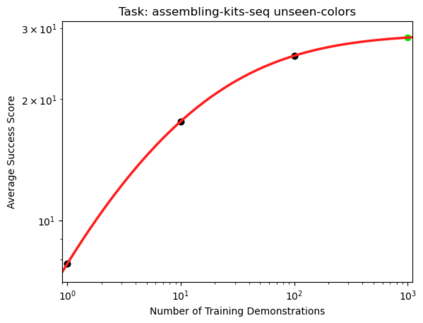
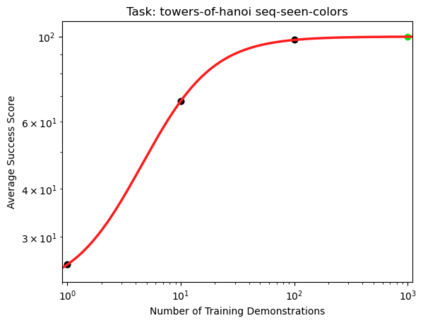
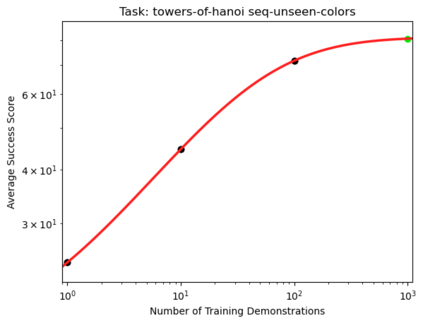
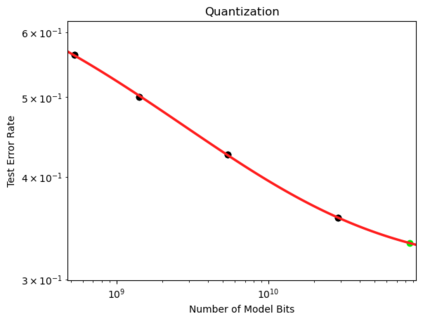
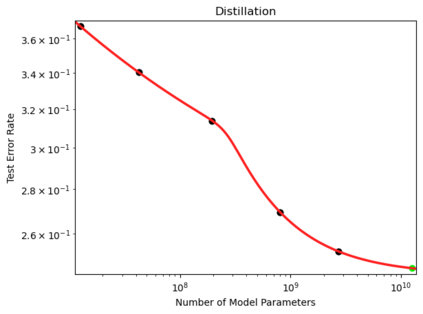
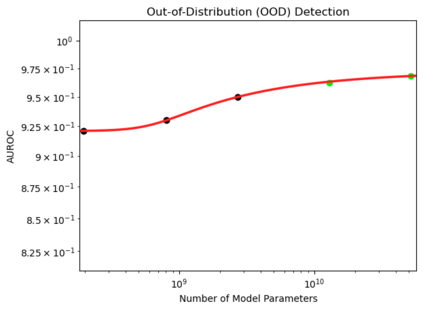
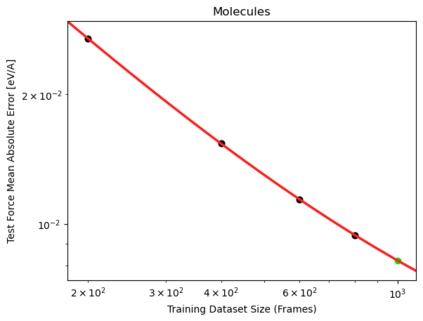
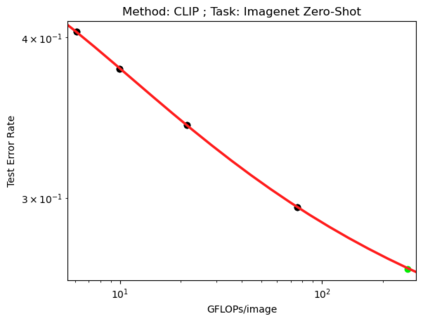
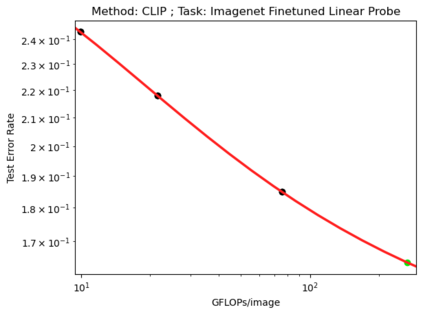
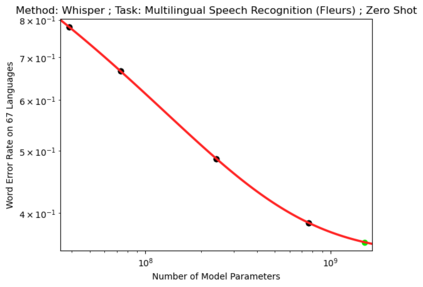
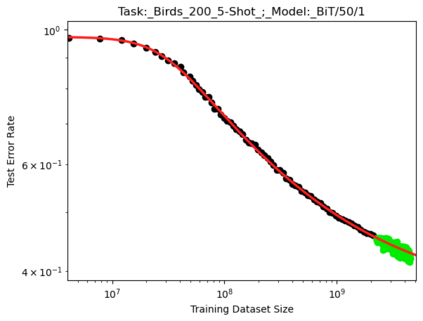
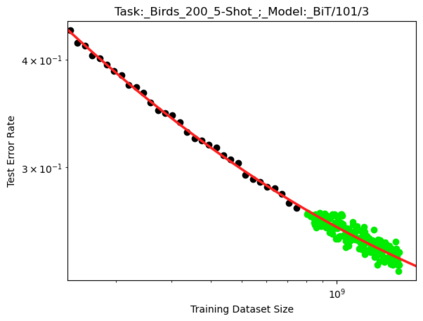
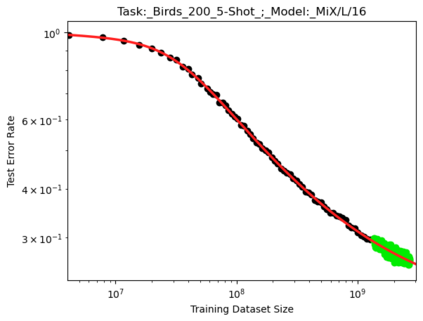
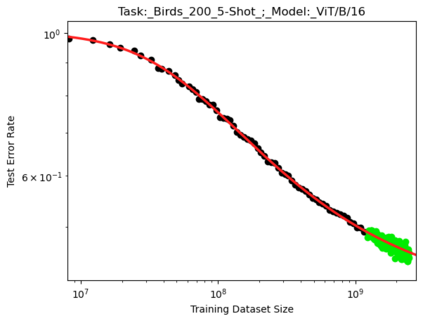
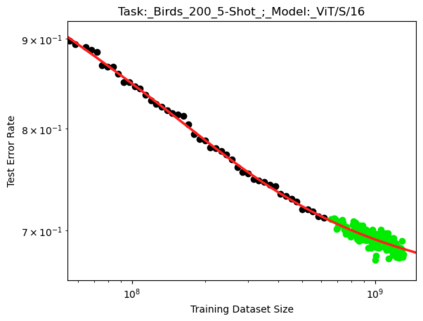
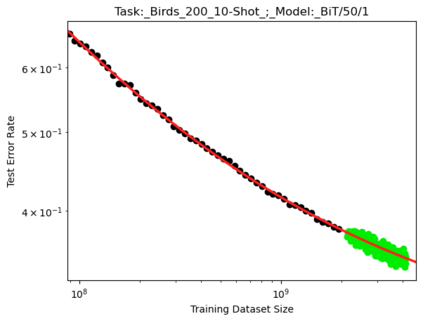
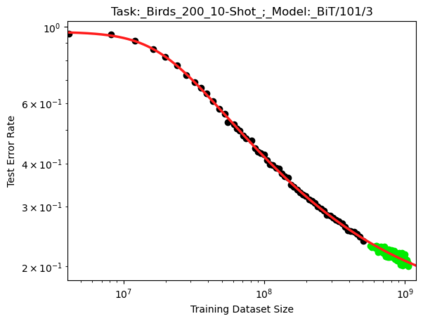
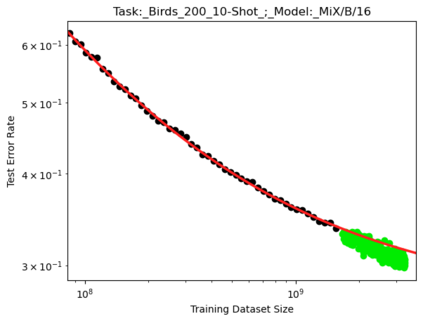
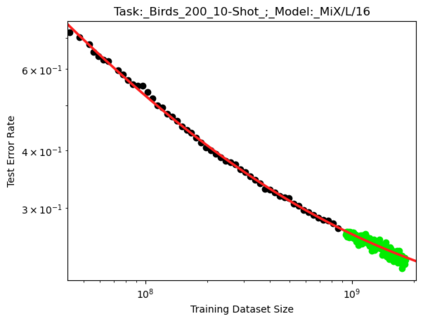
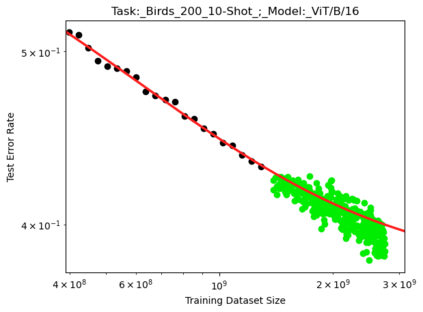
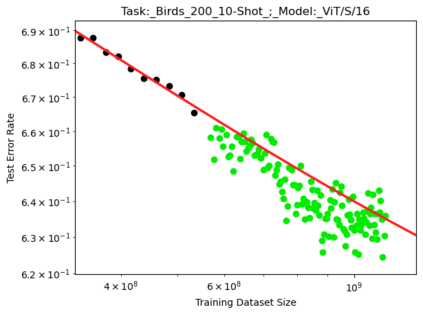
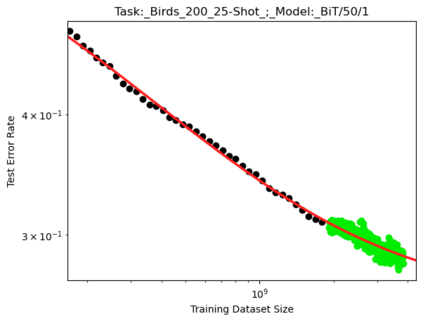
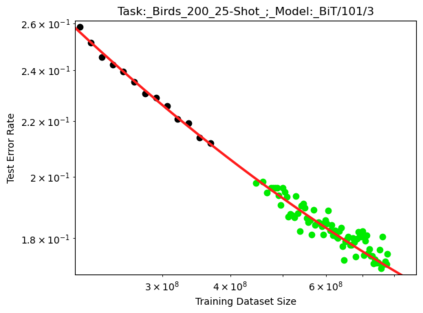
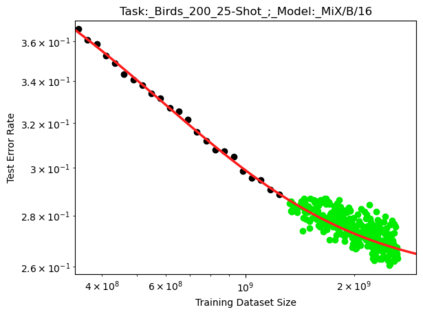
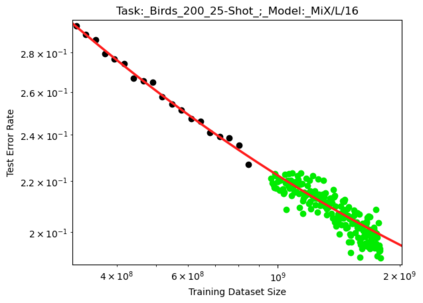
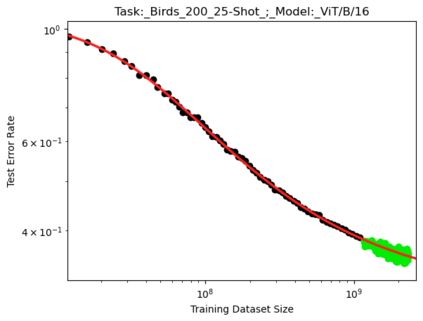
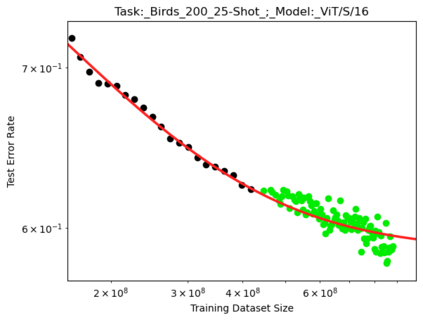
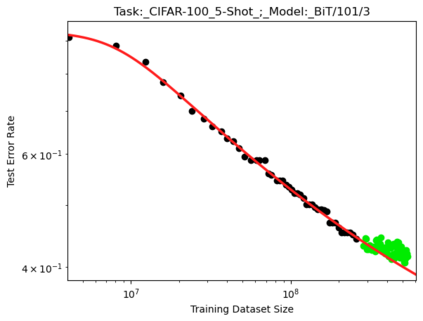
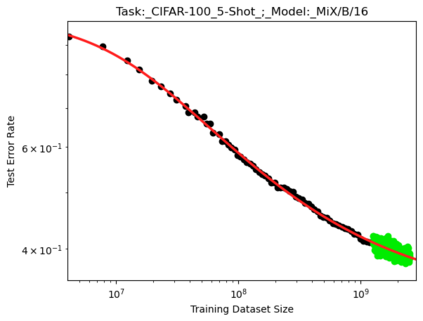
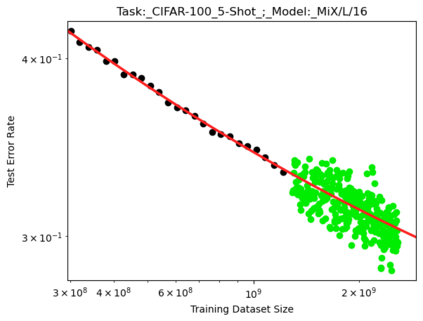
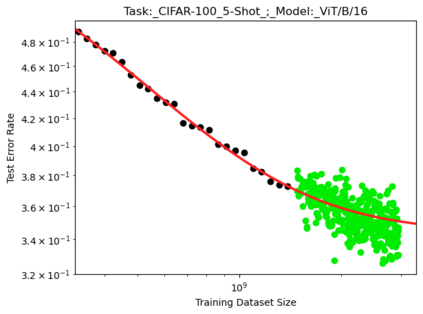
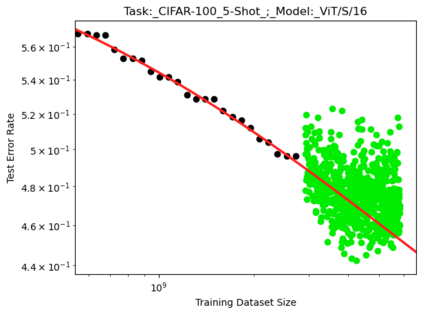
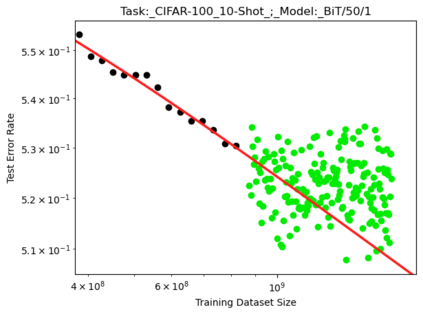
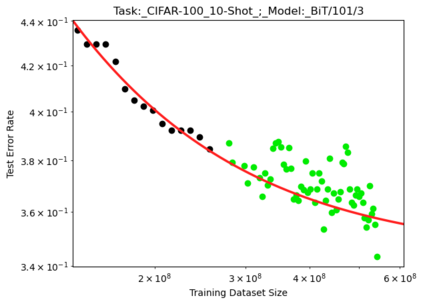
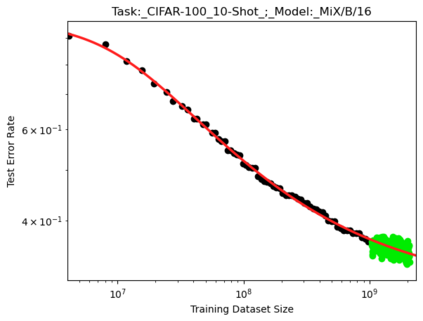
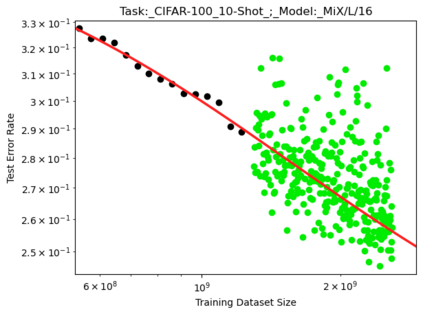
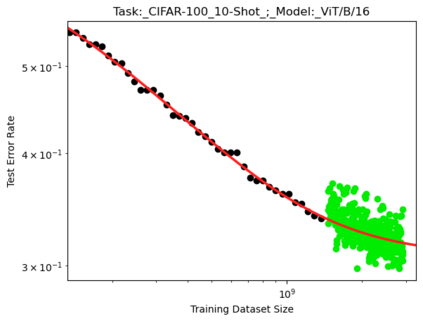
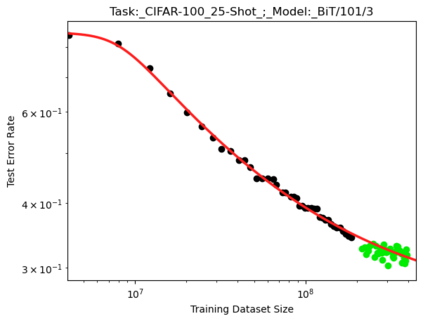
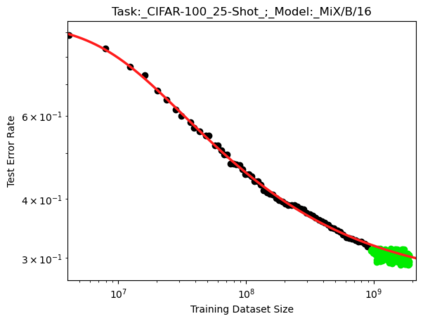
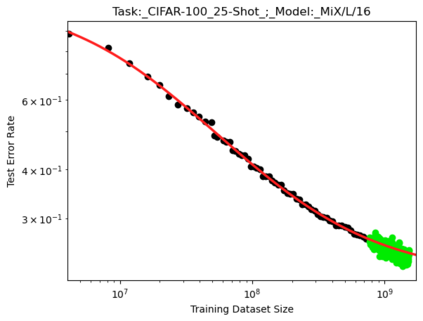
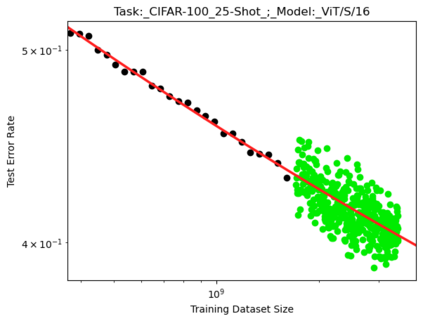
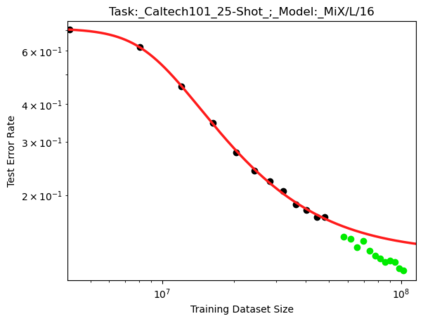
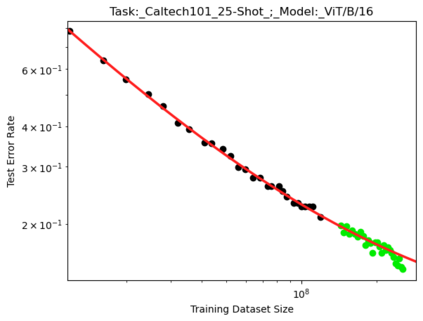
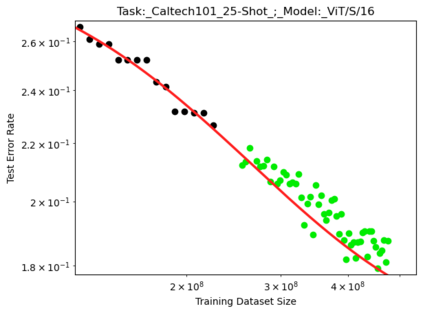
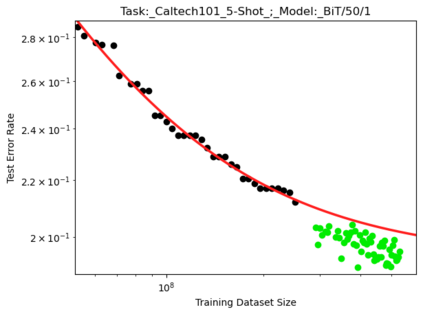
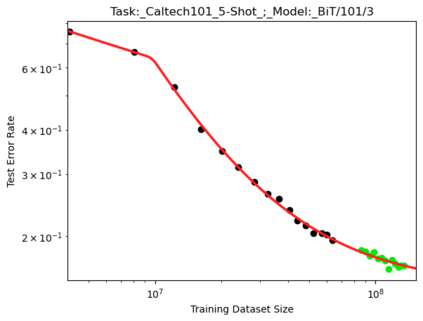
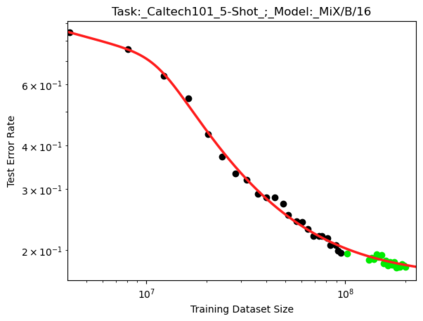
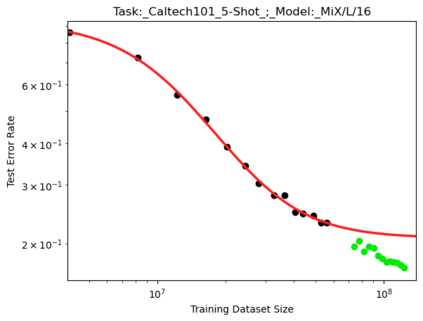
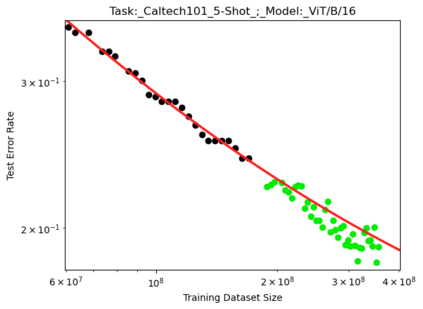
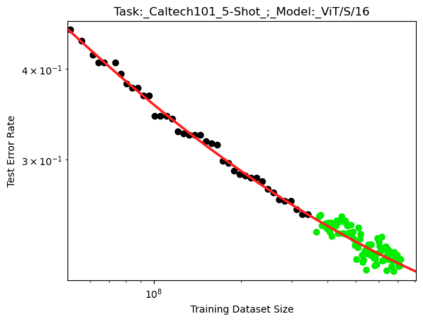
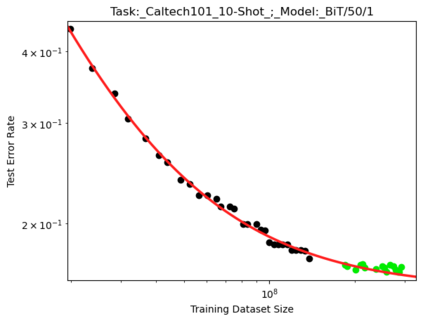
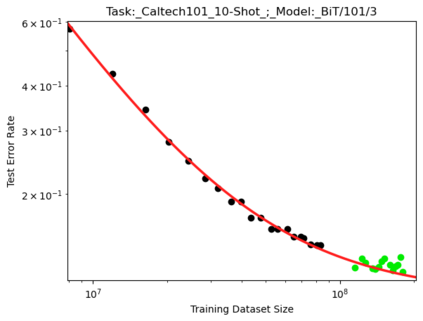
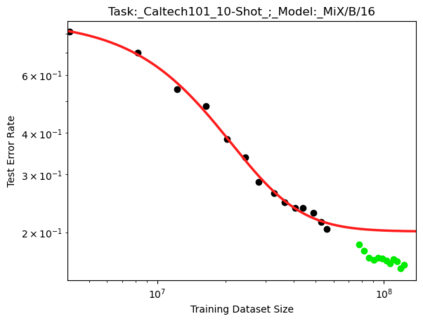
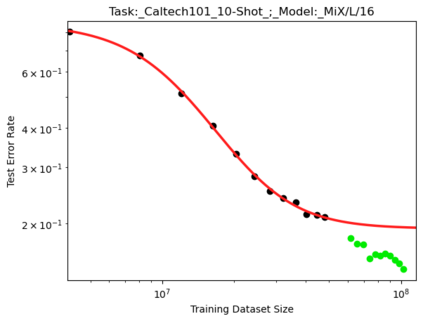
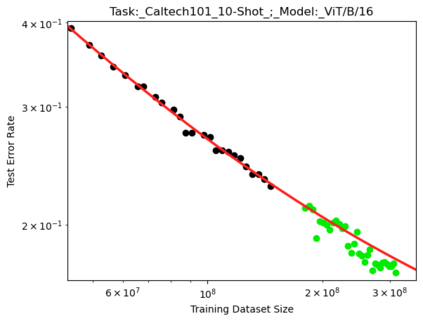
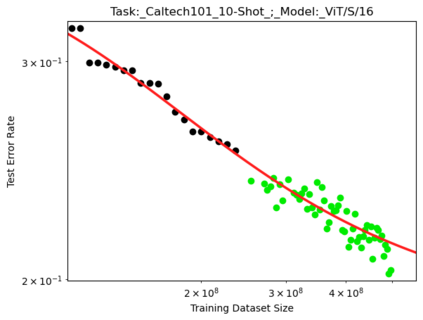
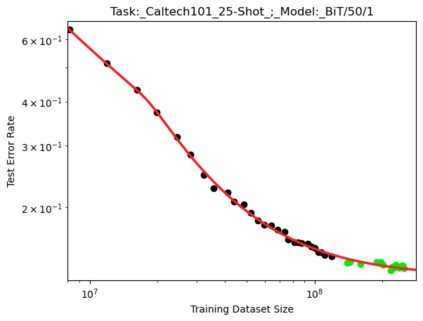
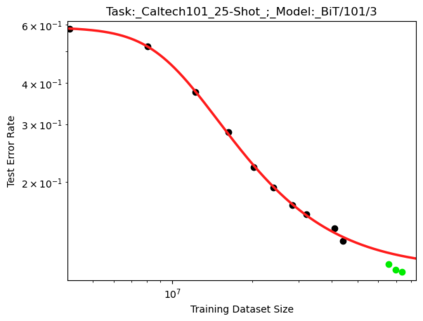
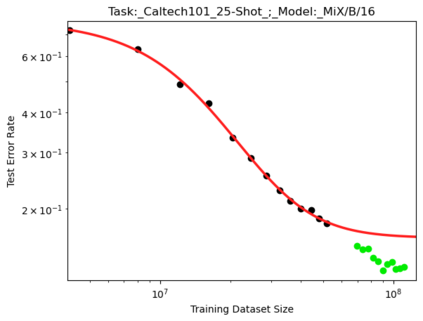
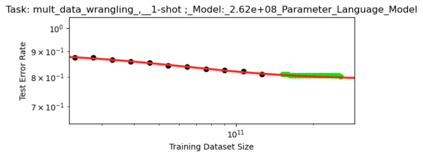
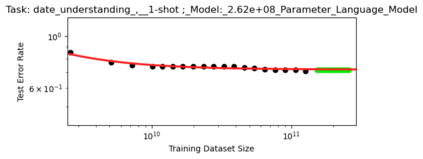
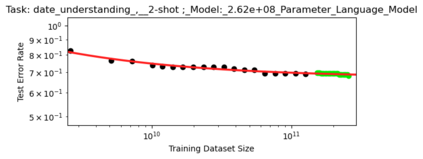
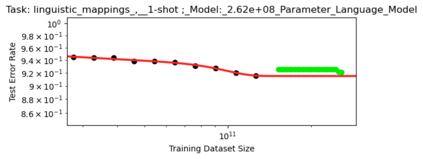
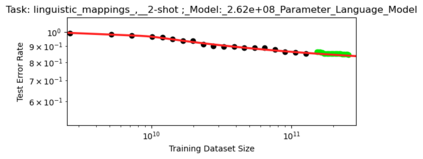
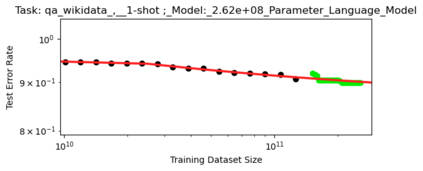
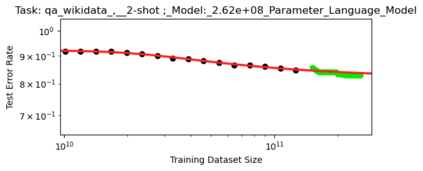
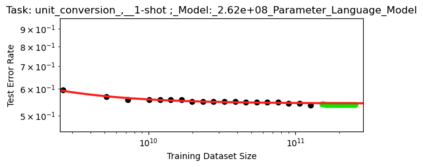
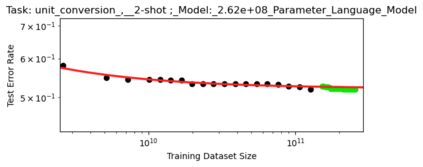
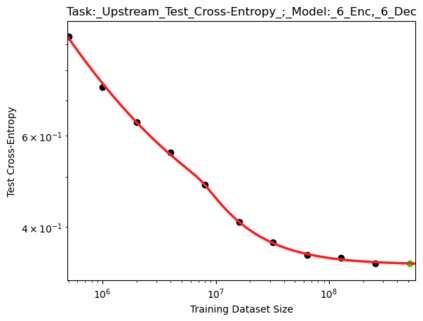
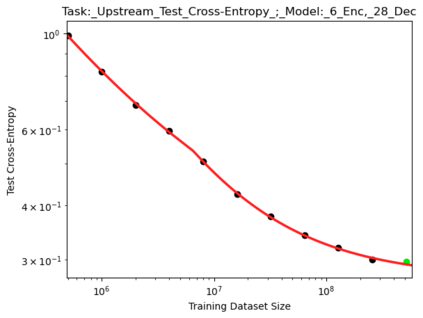
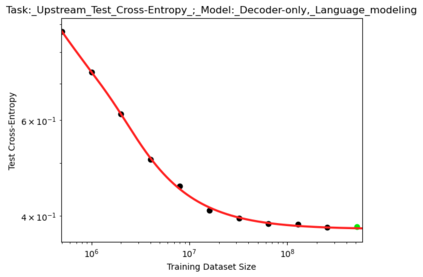
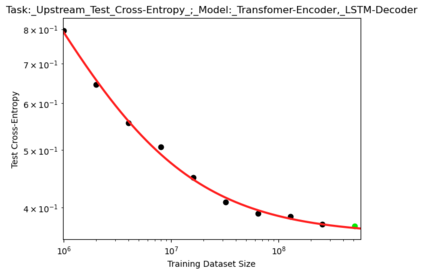
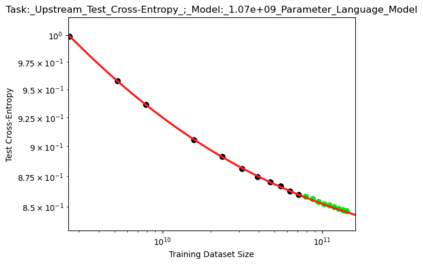
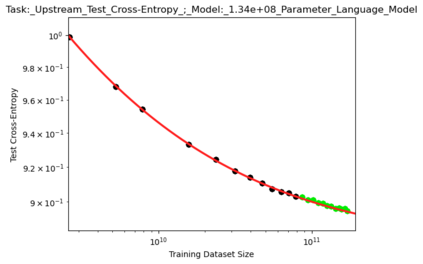
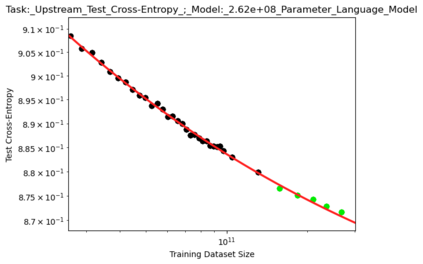
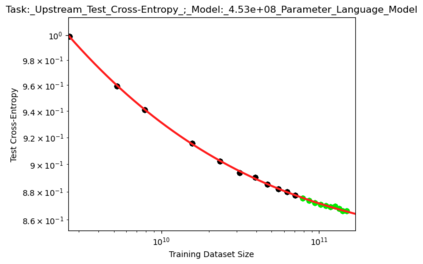
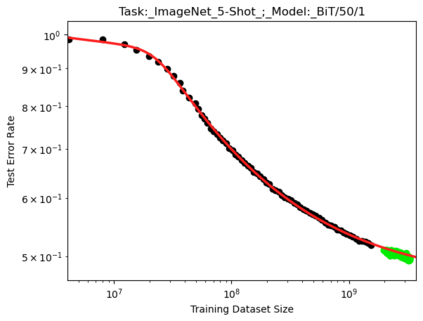
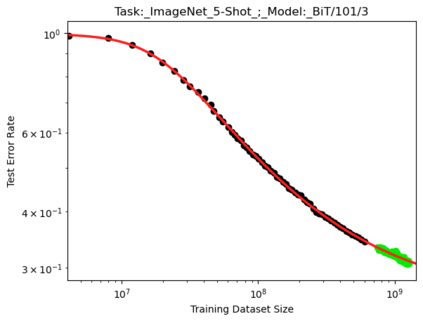
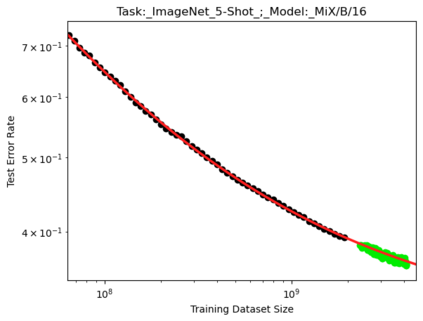
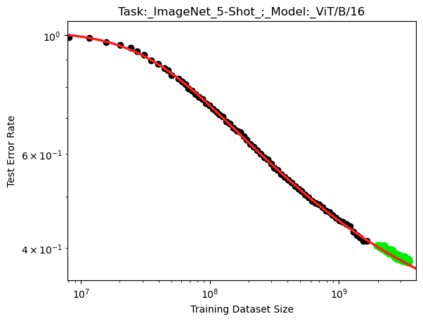
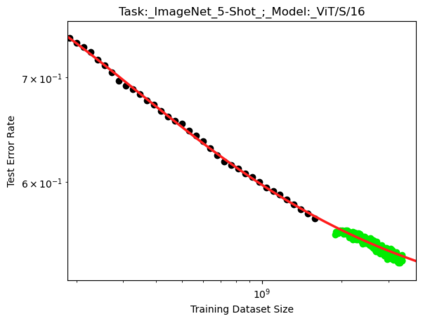
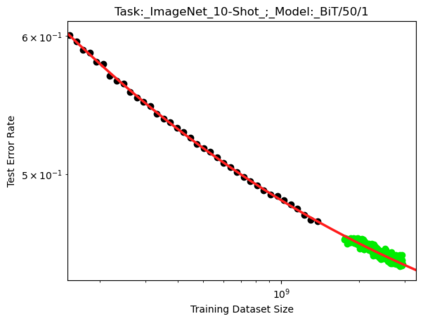
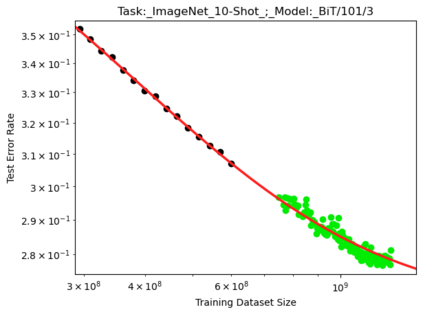
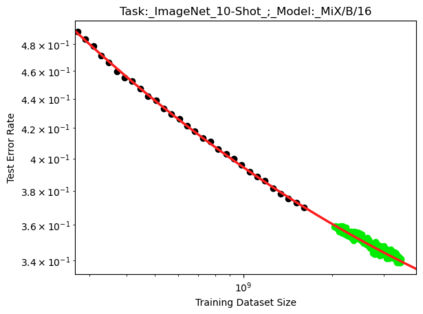
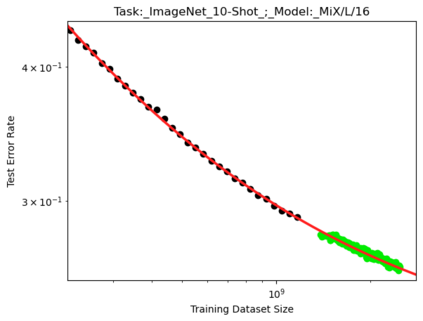
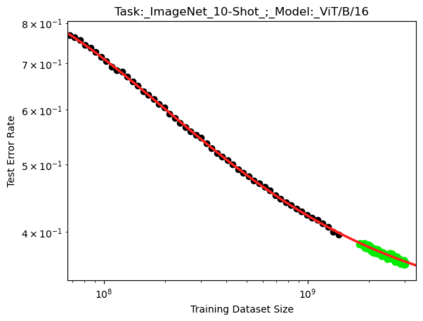
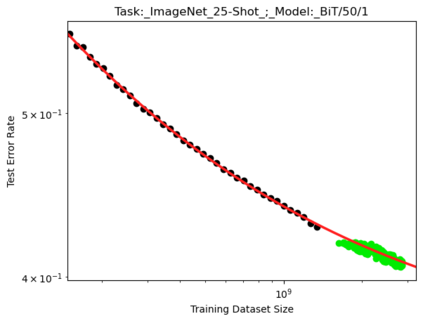
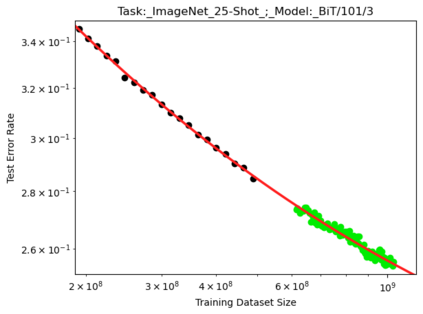
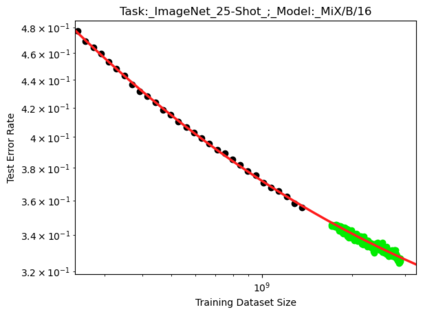
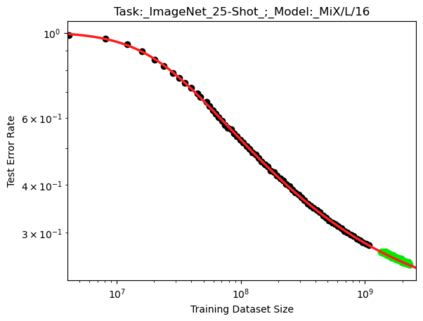
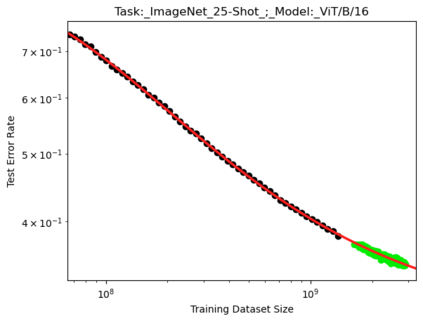
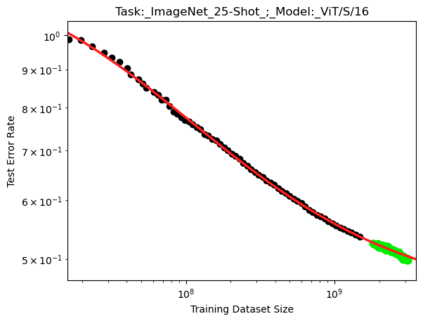
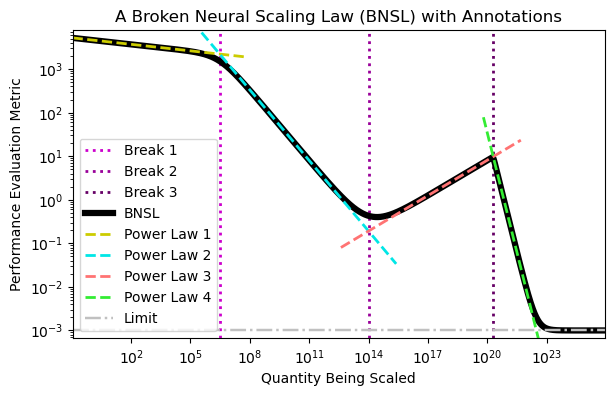
We present a smoothly broken power law functional form (referred to by us as a Broken Neural Scaling Law (BNSL)) that accurately models and extrapolates the scaling behaviors of deep neural networks (i.e. how the evaluation metric of interest varies as the amount of compute used for training, number of model parameters, training dataset size, model input size, number of training steps, or upstream performance varies) for various architectures and for each of various tasks within a large and diverse set of upstream and downstream tasks, in zero-shot, prompted, and fine-tuned settings. This set includes large-scale vision, language, audio, video, diffusion, generative modeling, multimodal learning, contrastive learning, AI alignment, robotics, out-of-distribution (OOD) generalization, continual learning, transfer learning, uncertainty estimation / calibration, out-of-distribution detection, adversarial robustness, distillation, sparsity, retrieval, quantization, pruning, molecules, computer programming/coding, math word problems, arithmetic, unsupervised/self-supervised learning, and reinforcement learning (single agent and multi-agent). When compared to other functional forms for neural scaling behavior, this functional form yields extrapolations of scaling behavior that are considerably more accurate on this set. Moreover, this functional form accurately models and extrapolates scaling behavior that other functional forms are incapable of expressing such as the non-monotonic transitions present in the scaling behavior of phenomena such as double descent and the delayed, sharp inflection points (often called "emergent phase transitions") present in the scaling behavior of tasks such as arithmetic. Lastly, we use this functional form to glean insights about the limit of the predictability of scaling behavior. Code is available at https://github.com/ethancaballero/broken_neural_scaling_laws