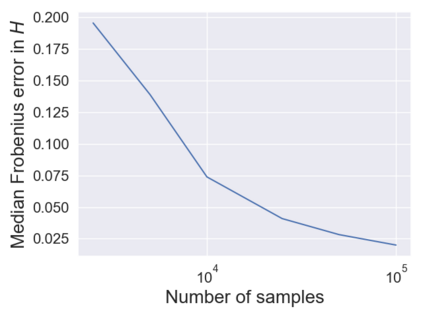
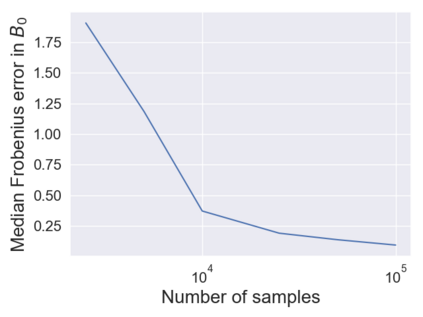
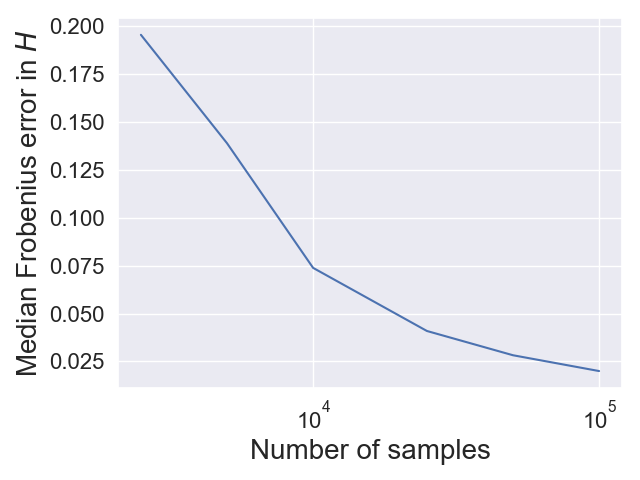
Causal disentanglement seeks a representation of data involving latent variables that relate to one another via a causal model. A representation is identifiable if both the latent model and the transformation from latent to observed variables are unique. In this paper, we study observed variables that are a linear transformation of a linear latent causal model. Data from interventions are necessary for identifiability: if one latent variable is missing an intervention, we show that there exist distinct models that cannot be distinguished. Conversely, we show that a single intervention on each latent variable is sufficient for identifiability. Our proof uses a generalization of the RQ decomposition of a matrix that replaces the usual orthogonal and upper triangular conditions with analogues depending on a partial order on the rows of the matrix, with partial order determined by a latent causal model. We corroborate our theoretical results with a method for causal disentanglement that accurately recovers a latent causal model.
翻译:原因解剖寻求通过因果模型来代表与彼此相关的潜在变量相关的数据。 如果潜伏模型和从潜伏变量向观察到变量的转变是独特的, 则代表可以识别。 在本文中, 我们研究观察到的变量是线性潜在因果模型的线性变异。 干预数据对于可识别性是必要的: 如果缺少一个潜在变量, 我们显示存在无法区分的不同模型。 相反, 我们证明每个潜在变量的单一干预足以识别。 我们的证据使用一个总化的 RQ 分解矩阵, 以根据矩阵行中部分顺序、 由潜在因果模型确定的部分顺序, 以类比取代常规或直角和上三角条件。 我们用一个准确恢复潜在因果模型的因果关系分解方法来证实我们的理论结果。