How to measure things

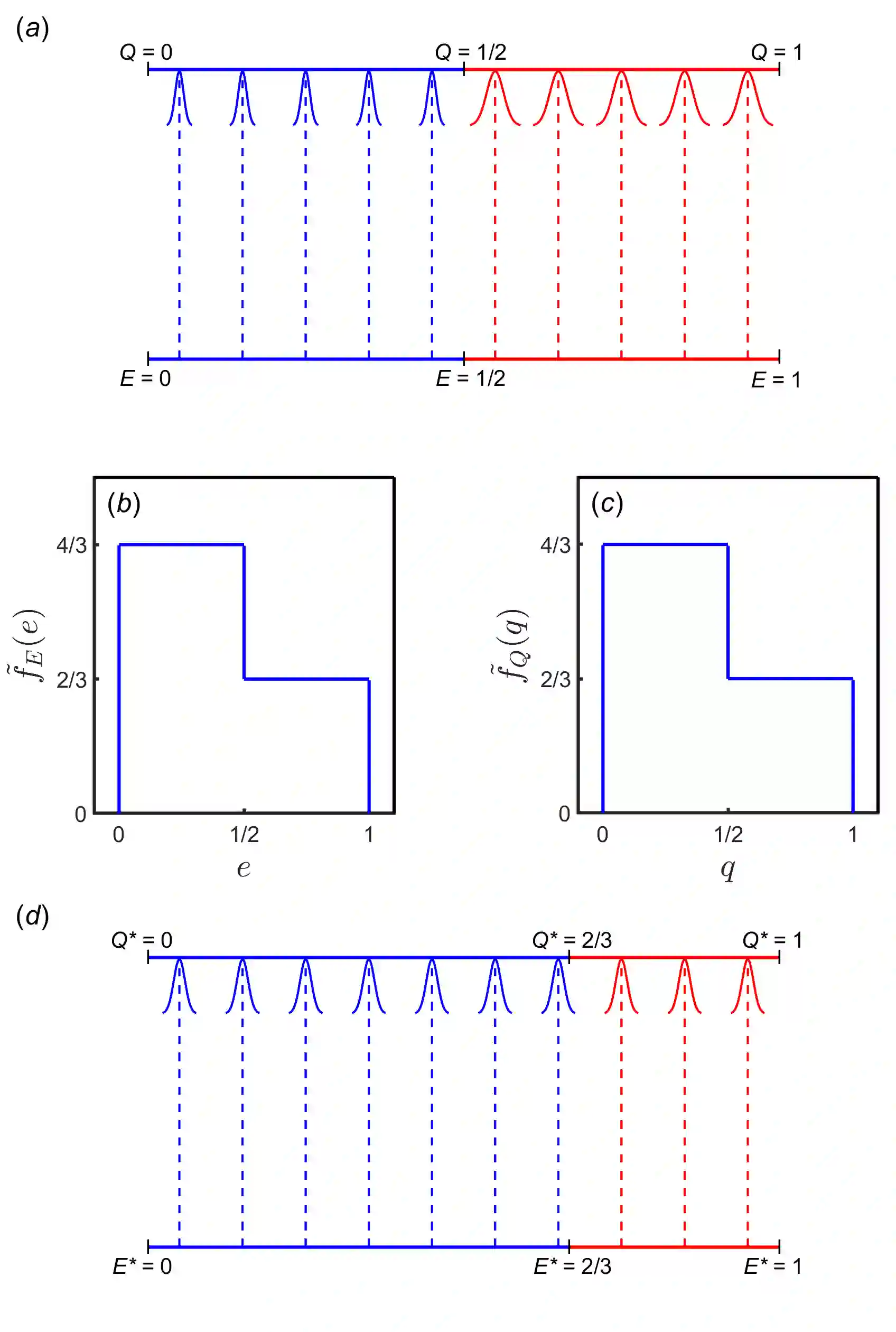
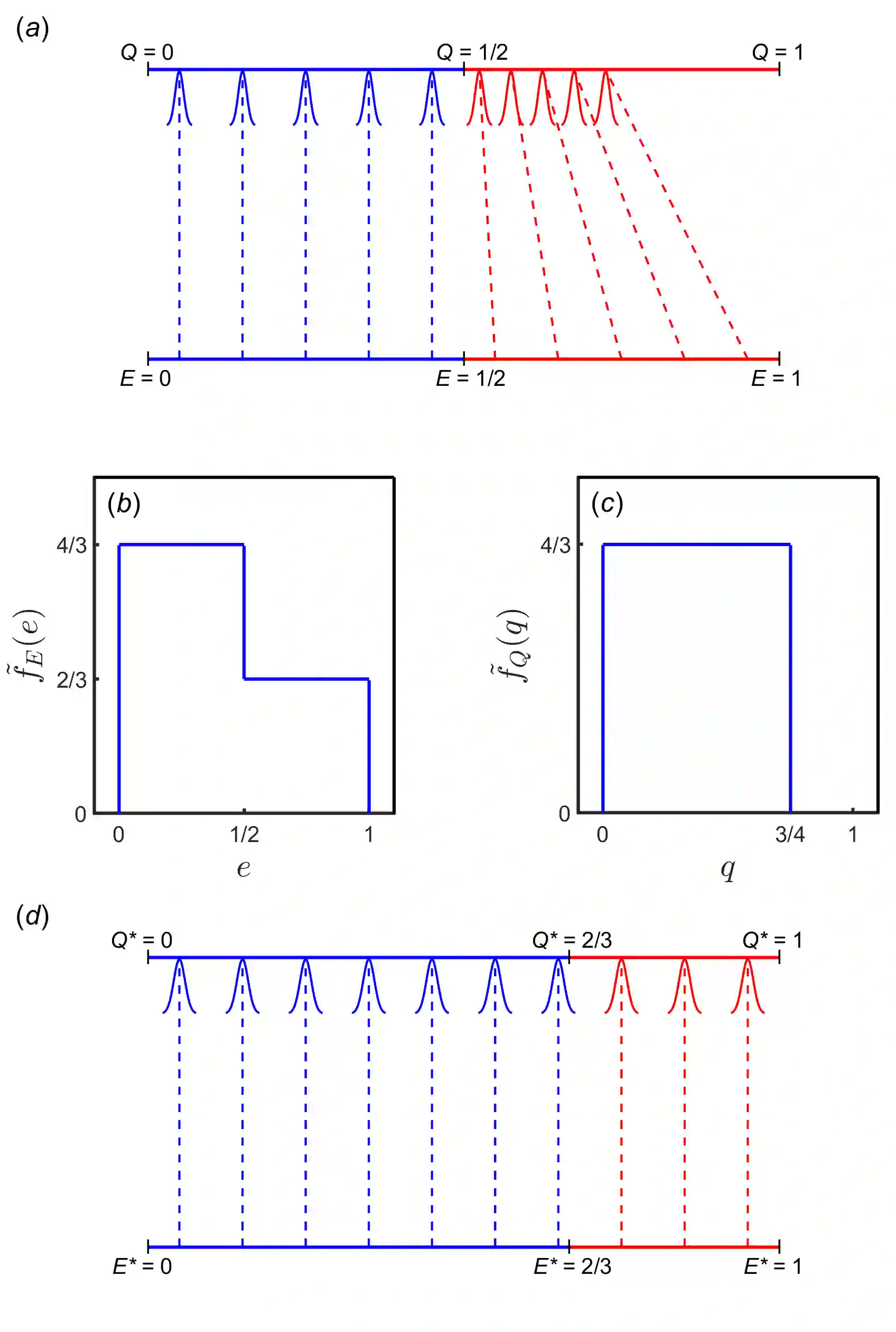
In classical information theory, a causal relationship between two random variables is typically modelled by assuming that, for every possible state of one of the variables, there exists a particular distribution of states of the second variable. Let us call these two variables the causal and caused variables, respectively. We assume that both of these random variables are continuous and one-dimensional. Carrying out independent transformations on the causal and caused variable creates two new random variables. Here, we consider transformations that are differentiable and strictly increasing. We call these increasing transformations. If, for example, the mass of an object is a caused variable, a logarithmic transformation could be applied to produce a new caused variable. Any causal relationship (as defined here) is associated with a channel capacity, which is the maximum rate that information could be sent if the causal relationship was used as a signalling system. Channel capacity is unaffected when the variables are changed by use of increasing transformations. For any causal relationship we show that there is always a way to transform the caused variable such that the entropy associated with the caused variable is independent of the value of the causal variable. Furthermore, the resulting universal entropy has an absolute value that is equal to the channel capacity associated with the causal relationship. This observation may be useful in statistical applications, and it implies that, for any causal relationship, there is a `natural' way to transform a continuous caused variable. With additional constraints on the causal relationship, we show that a natural transformation of both variables can be found such that the transformed system behaves like a good measuring device, with the expected value of the caused variable being approximately equal to the value of the causal variable.