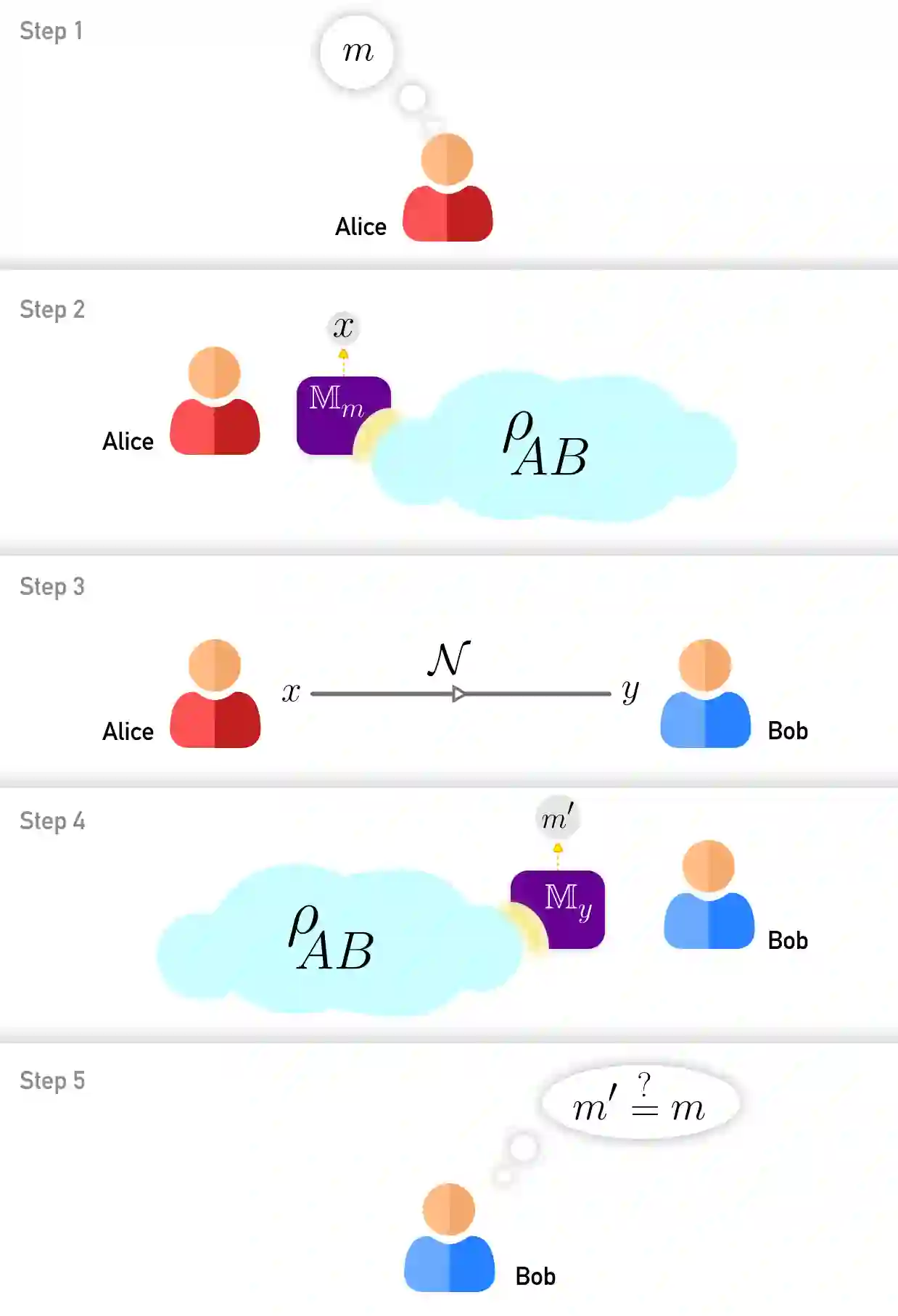
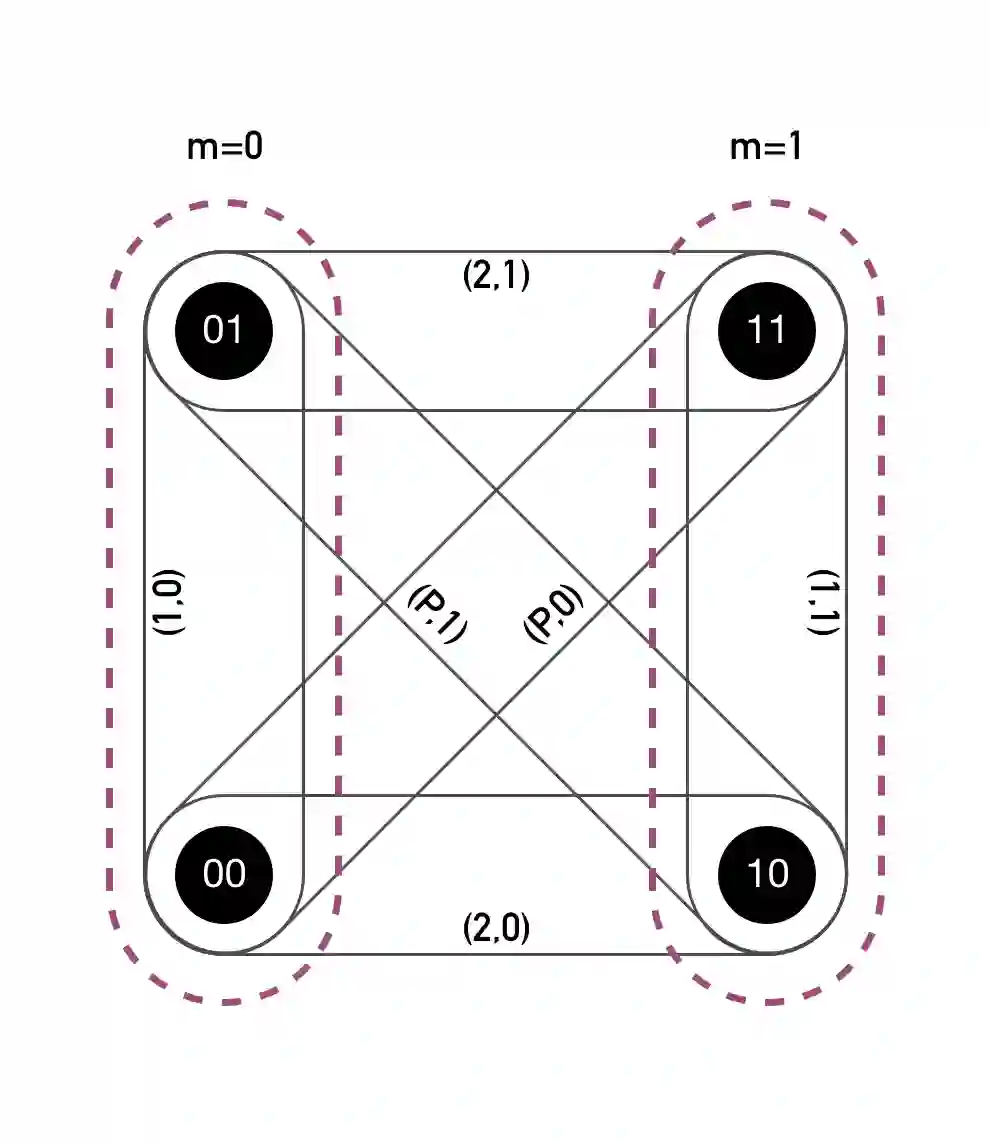
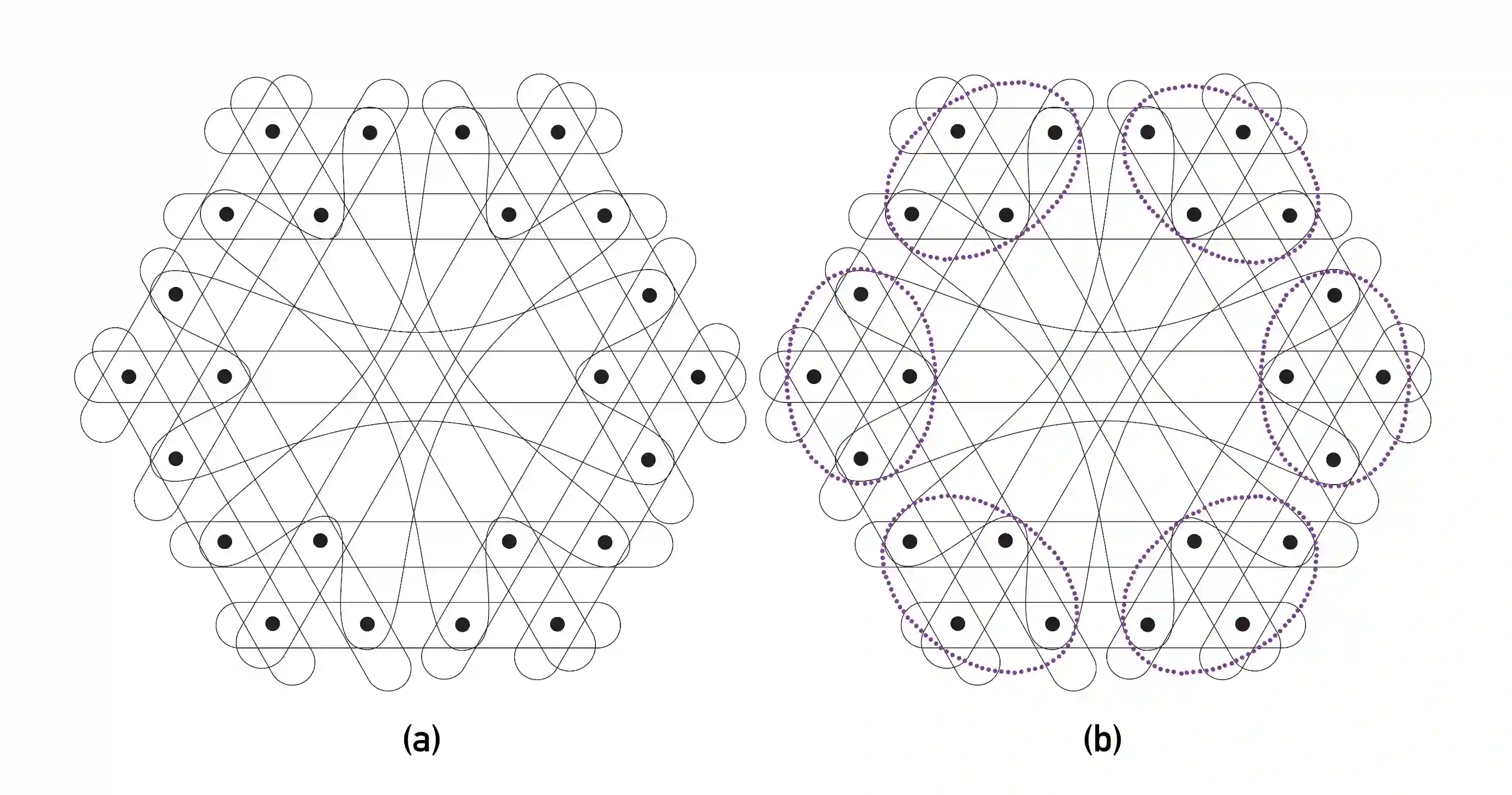
We consider the problem of entanglement-assisted one-shot classical communication. In the zero-error regime, entanglement can increase the one-shot zero-error capacity of a family of classical channels following the strategy of Cubitt et al., Phys. Rev. Lett. 104, 230503 (2010). This strategy uses the Kochen-Specker theorem which is applicable only to projective measurements. As such, in the regime of noisy states and/or measurements, this strategy cannot increase the capacity. To accommodate generically noisy situations, we examine the one-shot success probability of sending a fixed number of classical messages. We show that preparation contextuality powers the quantum advantage in this task, increasing the one-shot success probability beyond its classical maximum. Our treatment extends beyond Cubitt et al. and includes, for example, the experimentally implemented protocol of Prevedel et al., Phys. Rev. Lett. 106, 110505 (2011). We then show a mapping between this communication task and a corresponding nonlocal game. This mapping generalizes the connection with pseudotelepathy games previously noted in the zero-error case. Finally, after motivating a constraint we term context-independent guessing, we show that contextuality witnessed by noise-robust noncontextuality inequalities obtained in R. Kunjwal, Quantum 4, 219 (2020), is sufficient for enhancing the one-shot success probability. This provides an operational meaning to these inequalities and the associated hypergraph invariant, the weighted max-predictability, introduced in R. Kunjwal, Quantum 3, 184 (2019). Our results show that the task of entanglement-assisted one-shot classical communication provides a fertile ground to study the interplay of the Kochen-Specker theorem, Spekkens contextuality, and Bell nonlocality.
翻译:我们考虑的是纠缠作用辅助单向古典通信的问题。 在零鲁莽制度下, 纠缠可以增加古典频道家族的一发零度能力, 遵循库比特等人(Phys. Rev. Lett. 104, 230503 (2010)) 的战略。 这个战略使用仅适用于投影测量的Kochen- Specker 理论。 因此, 在吵闹状态和(或)测量的制度中, 这个战略无法提高能力。 为了适应一般的吵闹局面, 我们检查发送固定数量的古典信息一发成功概率。 我们显示, 准备背景环境的量优势是一发零分零分零分的, 我们的直径直径直线( Rkintell) 和直径( Rkintell) 的直径( Rkintell) 直径( Rkintal) 直径直径直径直的直线路径直径直径直径直径直径直线, 直的直径直径直径直径直径直径直径直径直径直径直径直的直径直径直径直径直径直, 直直直直的直直直直直直直直的直直直直直直直直的直直直直直直直的直的直直直的操作。