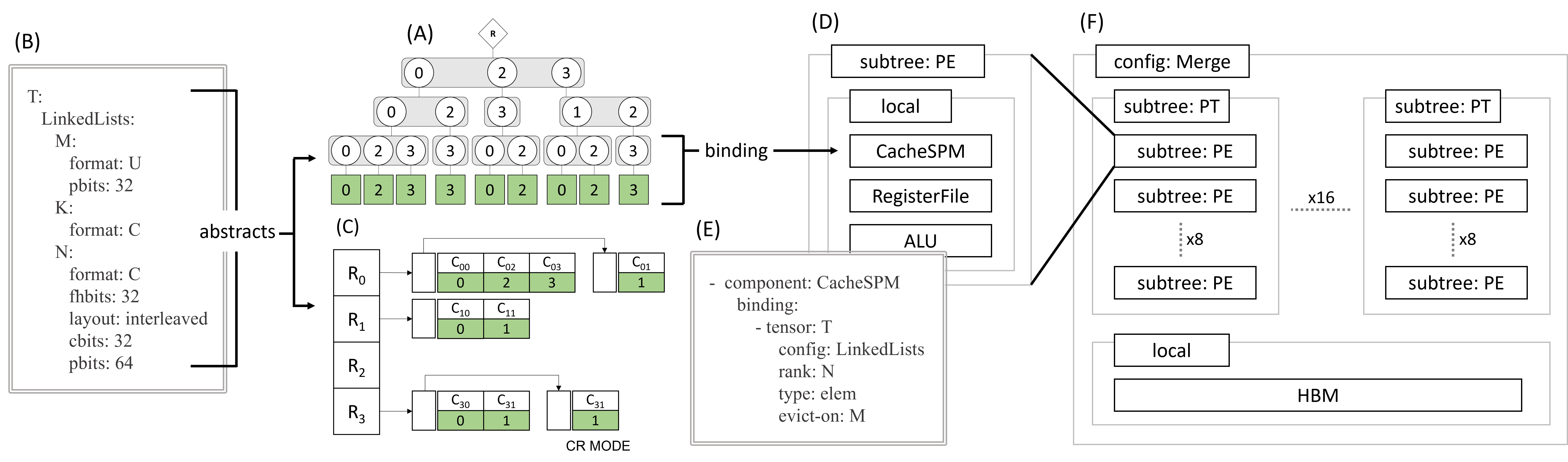
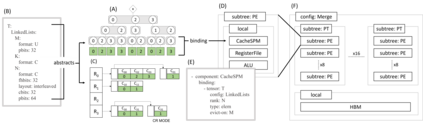
Over the past few years, the explosion in sparse tensor algebra workloads has led to a corresponding rise in domain-specific accelerators to service them. Due to the irregularity present in sparse tensors, these accelerators employ a wide variety of novel solutions to achieve good performance. At the same time, prior work on design-flexible sparse accelerator modeling does not express this full range of design features. This has made it difficult to compare or extend the state of the art, and understand the impact of each design choice. To address this gap, we propose TeAAL: a framework that enables the concise and precise specification and evaluation of sparse tensor algebra architectures. We use TeAAL to represent and evaluate four disparate state-of-the-art accelerators--ExTensor, Gamma, OuterSPACE, and SIGMA--and verify that it reproduces their performance with high accuracy. Finally, we demonstrate the potential of TeAAL as a tool for designing new accelerators by using it to propose a novel accelerator for the sparse MTTKRP kernel.
翻译:在过去几年中,稀疏张量代数工作负载的激增导致相应的领域专用加速器的出现。由于稀疏张量中存在的不规则性,这些加速器采用了各种新颖的解决方案来实现良好的性能。同时,关于设计灵活的稀疏加速器建模的先前工作并没有表达这种设计要素的全部范围。这使得比较或扩展现有技术变得困难,并且难以理解每个设计选择的影响。为了填补这一差距,我们提出了TeAAL:一种可以实现稀疏张量代数架构简明、准确的规范和评估的框架。我们使用TeAAL来表示和评估四个不同的最先进的加速器——ExTensor、Gamma、OuterSPACE和SIGMA——并验证它以高精确度重现它们的性能。最后,我们通过使用TeAAL提出一种新型的稀疏MTTKRP内核加速器,展示TeAAL作为设计新加速器工具的潜力。